Ce post fait suite à un autre posté récemment sur mélaudia dont le sujet était le filtrage à 6 dB du système de Kaneda. Je le reprends en le généralisant au problème de la maîtrise de la distorsion de phase.
------------------------------------------------------------------------------------------------------
Vous pourrez trouvez deux synthèses sur le filtrage FIR faite par Jean et JIM un peu plus loin dans les échanges - Dagda
------------------------------------------------------------------------------------------------------
Quel doit être l'objectif du filtrage : obtenir une réponse totale à phase minimale ou à phase linéaire ? On peut, pour répondre à cette question, poser préalablement celle-ci : une fonction de transfert peut-elle être simultanément à phase minimale et à phase linéaire ?
La théorie du signal permet évidemment de répondre à cette dernière question. Sans entrer trop dans les détails, on peut quand même énoncer quelques propriétés :
- un filtre à phase linéaire à une réponse impulsionnelle symétrique.
- un filtre à phase minimale à tous ses zéros de sa transformée en z strictement à l'intérieur du cercle unité.
- le caractère symétrique de la réponse impulsionnelle du filtre à phase linéaire implique que si z0 est un zéro de la transformée en z, alors 1/z0 est également un zéro.
- il n'y a donc qu'une possibilité pour qu'un filtre soit à la fois à phase linéaire et à minimum de phase : il faut que les zéros vaillent zéro !
- on en déduit que la fonction de transfert ne peut être qu'un gain pur avec un retard.
Nous noterons s , la variable de Laplace dont il faut simplement savoir qu'elle est liée à la pulsation (ou fréquence) du signal et normalisée par la fréquence de coupure du filtre concerné.
Considérons uniquement le cas de deux haut-parleurs, l'un filtré par un passe-bas (LP, low pass) et un autre filtré par un passe-haut (HP, high pass). Nous supposerons que les haut-parleurs utilisés sont parfaits, ce qui signifie qu'ils se modélisent par un gain pur.
On cherche à ce que la somme soit également un gain pur, ce qui se traduit par le fait que la somme des fonctions de transfert vaut 1. Cela signifie que la réponse en fréquence est plate, que le déphasage est nul. La réponse totale est donc bien à phase minimale et à phase linéaire.
Cela se traduit mathématiquement par :
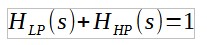
Examinons le cas du filtre du premier ordre. La fonction de transfert du passe bas s'écrit :
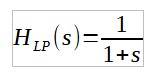
On déduit le filtre passe-haut en remplaçant s par 1/s ce qui nous donne :
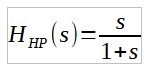
On peut à présent sommer les deux filtres et on obtient :
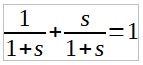
Ainsi, les filtres du premier ordre remplissent notre condition initiale et se traduisent par une réponse plate en amplitude et une phase nulle.
Cependant, concrètement cela ne fonctionne pas. Rappelons que nous avons supposé que les haut-parleurs étaient parfaits. Dans la pratique les haut-parleurs ont des fréquences de coupure haute et basse. Un filtrage aussi faible que 6 dB imposerait une bande passante très étendue de chaque haut-parleur ce qui est impossible.
Peut-on remplir notre condition initiale avec des filtres d'un ordre supérieur ?
Prenons par exemple un filtre de Linkwitz–Riley de 24 dB par octave à phase minimale. Les fonctions de transfert sont :
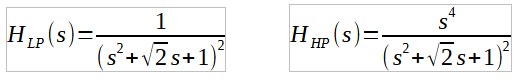
La somme donne :
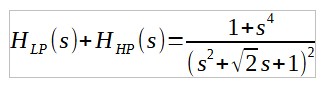
Cette somme ne vaut pas 1. On peut montrer que le module de cette somme vaut bien 1 mais qu'il y a des variations de phase.
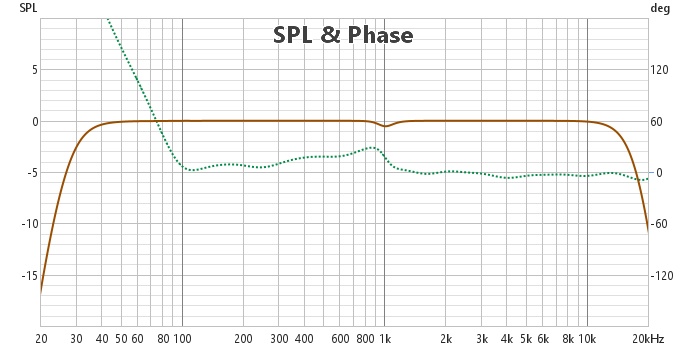
Pour s'en convaincre, on peut simuler ces deux filtres avec rePhase, les importer dans Rew et calculer leur somme. Voici ce que l'on obtient :
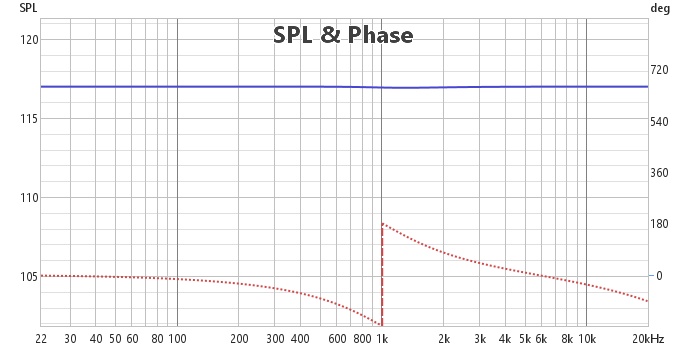
On remarque la distorsion de phase. La phase minimale de ce filtre est plate étant donné sa bande passante, ce qui signifie que la phase représentée est l'excess phase. Bien que les filtres passe-bas et passe-haut soient tous deux à phase minimale, la somme ne l'est pas.
Dès lors peut-on trouver des filtres d'ordre supérieur à 1 tels que notre condition initiale soit respectée ? L'idée (qu'ont eu des gens bien avant nous..) est de réaliser un filtre complémentaire.
On se donne un filtre passe-bas d'un ordre supérieur à 1 et on calcule le filtre passe-haut par :
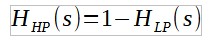
Faisons cet exercice avec un filtre passe-bas du second ordre quelconque. On obtient :
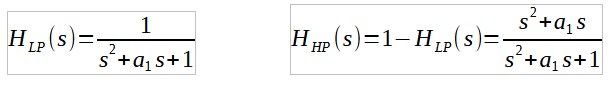
Il est alors intéressant d'examiner la pente de coupure du filtre passe-haut. Pour cela, on réalise un développement limité en 0 (basse fréquence) et l'on trouve :
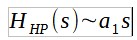
On retombe sur un filtre du premier ordre (la pente est de 6 dB par octave). On peut montrer qu'on obtient ce résultat quel que soit l'ordre du filtre passe-bas. On est revenu à la case départ.
Voilà où nous en étions avec le filtrage analogique, mais l'avènement du filtrage numérique va bien changer les choses !
Prenons un filtre passe-bas à réponse impulsionnelle finie (FIR) à phase linéaire. Celui-ci s'exprime par :
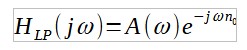
avec n0 qui modélise le retard du filtre. En prenant le filtre passe-haut suivant :
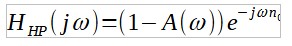
la somme des filtres vérifie bien notre condition initiale. Il s'agit d'un filtre à phase linéaire de même retard de phase.
Cependant nous pouvons maintenant choisir le type de filtre, la pente que nous voulons (permettant de limiter les recouvrements des haut-parleurs), aligner les bouches des pavillons en compensant numériquement les retards des voies.
Pour se convaincre de la réalité de ces calculs, voici la simulation de la somme de deux filtres à phase linéaire Linkwitz–Riley de 24 dB. On constate que l'amplitude de la somme vaut bien 1 et que la phase est nulle en tous points :
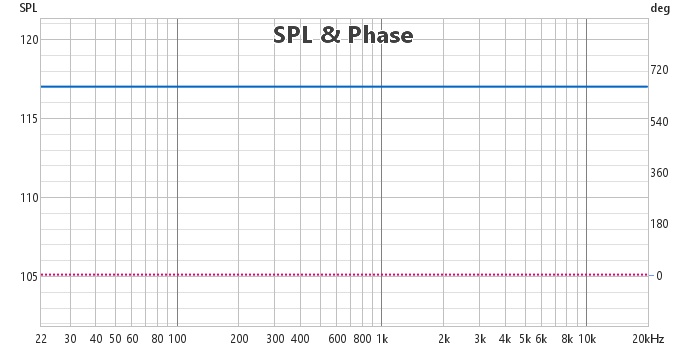
Ce système est simultanément à phase minimale et à phase linéaire. C'est un gain pur avec retard, retard introduit par le filtrage FIR.
Abordons à présent le cas de haut-parleurs plus réalistes ayant eux-mêmes une bande passante. Nous examinerons toujours le cas d'un système à deux voies et modéliserons chaque haut-parleur par un passe-bande avec une fréquence de coupure haute et basse modélisées chacune par un filtre Linkwitz–Riley de 24 dB.
Voici la réponse des deux haut-parleurs :
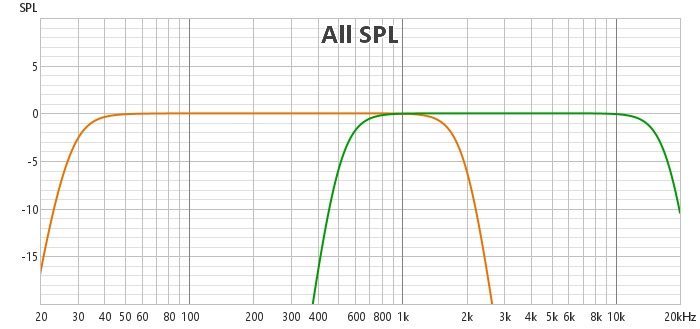
Les fréquences de coupure des haut-parleurs sont choisies pour qu'ils se recouvrent à 1 khz qui sera la fréquence de coupure du filtre devant les réunir.
On sait déjà que le système résultant ne sera pas à la fois à phase minimale et linéaire puisque ce n'est pas un gain pur. En effet, la fréquence de coupure basse du haut-parleur de grave ainsi que la fréquence de coupure haute du haut-parleur d'aigu subsisteront. Cependant est-il possible que dans une bande plus réduite que la bande passante totale de ce système la réponse puisse être à la fois à phase minimale et à phase linéaire ?
On va pour cela calculer un filtrage FIR à phase linéaire avec rePhase en linéarisant la phase autour de la fréquence de coupure prévue de 1khz.
Voici ce que l'on obtient pour les basses :
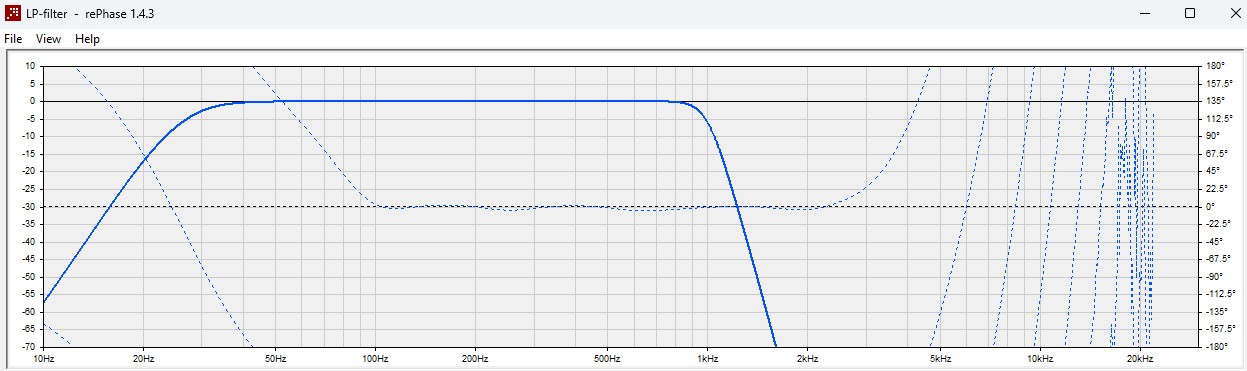
Le filtrage FIR est de 100 dB/octave. Nous avons linéarisé la phase jusqu'à 100 hz.
Le résultat pour les aigus :
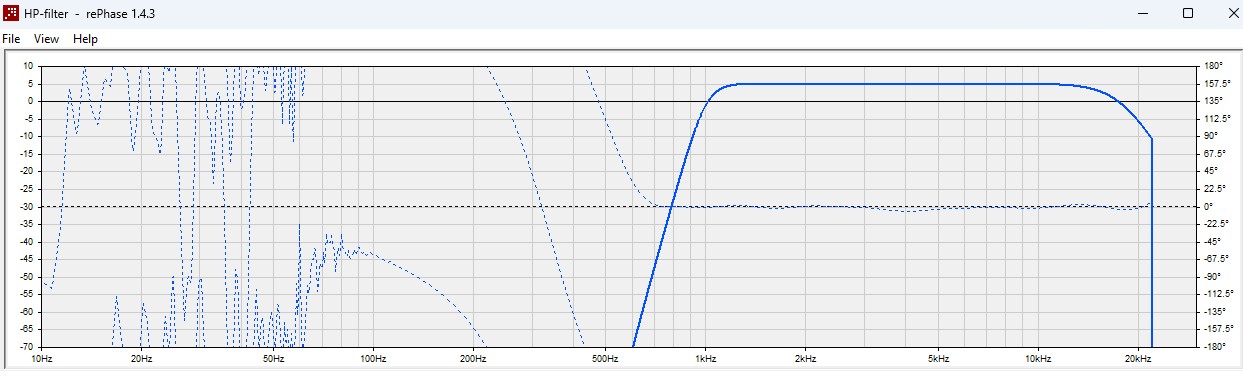
Le filtrage FIR est toujours de 100 dB/octave mais dans ce cas nous avons linéarisé la phase y compris jusqu'à la fréquence de coupure haute du haut-parleur.
Il nous reste à générer la réponse impulsionnelle de ces deux filtres, les exporter dans REW, calculer le produit de convolution de ces deux filtres avec les réponses des haut-parleurs correspondants et sommer ces deux réponses. Voici ce que l'on obtient :
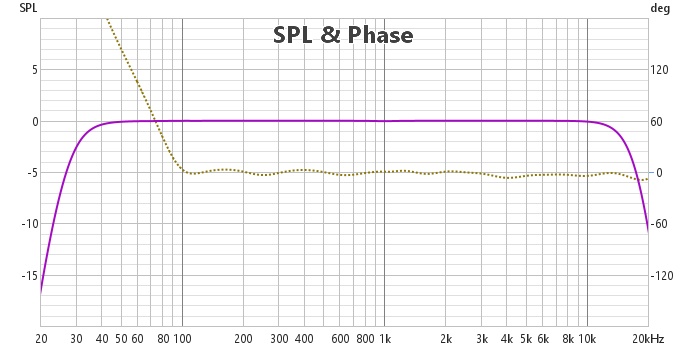
La réponse en fréquence est évidemment parfaite et la phase linéaire de 100 hz à 20 khz.
Qu'en est-il de la phase minimale ? Voici le tracé de la phase minimale superposée à la phase :
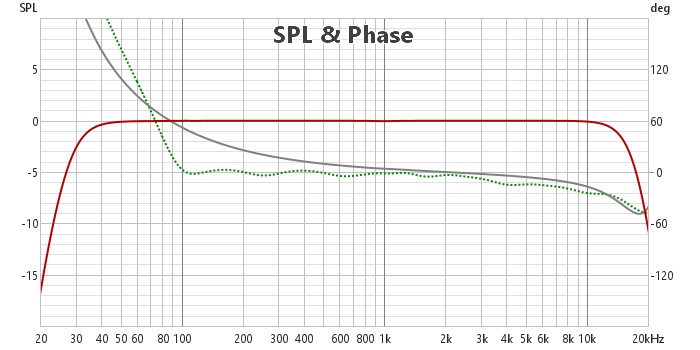
On constate que le filtre est quasiment à phase minimale de 300 hz à 20 khz.
C'est dans les basses fréquences que l'écart est le plus important (100 hz -300 hz), ce qui n'est pas étonnant puisque nous avions linéariser la phase jusqu'à 100 hz.
Voici la courbe de l'excess phase où l'on constate bien cet écart dans la bande 100 hz 300 hz.
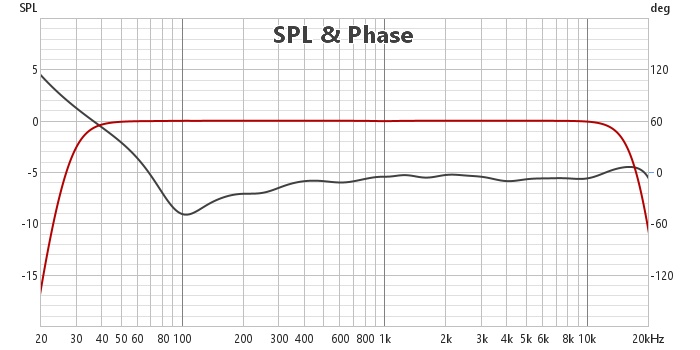
Nous avons obtenu un système simultanément à phase linéaire et minimale de 300 hz à 20 khz.
Ci-joint le fichier mdat pour ceux qui voudraient approfondir où faire des manips : fichier REW
Cordialement
Jean