Sound Pixel Lab

Bonjour à tous,

Pour traiter le problème des BF, une solution intéressante, déjà débattue, consiste à utiliser un SBA. L'idée est d'avoir un front d'onde quasi plan avec des positions de HP qui n'excite pas les modes.  Il faut pour cela que les murs latéraux proches des HP ne soient pas trop absorbants dans la bande de fonctionnement du SBA.

Une autre solution consiste à ne pas tenter de créer une onde plane, mais à essayer au contraire de la rendre la plus directive possible. Une solution est alors de placer une line array. Le problème est : à partir de quelle largeur la line array devient-elle directive dans les BF ?


Considérations générales :

Le schéma suivant montre la propagation des ondes d'une line array :


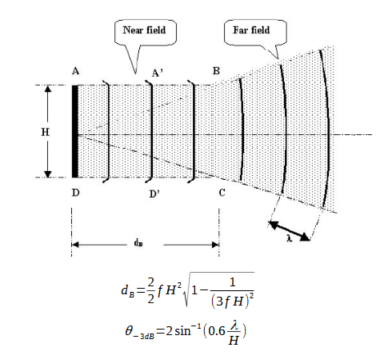
Sur la distance dB l'onde est quasi plane et chute de -3dB quand la distance double (near field). Au-delà, l'onde est sphérique et chute de -6dB quand la distance double (far field). Notons que la chute de -3dB dans la zone near field est due au phénomène d'interférence et s'accompagne d'oscillation dans cette bande.

Les formules ci-dessus permettent de calculer la longueur de la zone dB et l'angle à -3dB de directivité dans le far field. Dans ces formules, H est la longueur de la line array, F la fréquence en kHz et lambda la longueur d'onde en mètre.

L'argument de la racine carrée devant être positif, on déduit, pour une line array de longueur donnée, la fréquence minimum pour qu'il existe une zone near field. Ainsi, pour une line array de 11 m, cette fréquence vaut 30hz et passe à 55 hz pour une de ligne de 5m.

À une fréquence de 60 hz, l'angle thêta vaut 36 degrés pour une ligne de 11 m et 87 degrés pour une ligne de 5 m.

Le fichier Excel ci-joint permet de calculer les caractéristiques d'une line array en fonction de F et H : Line array.xls

On constate évidemment que plus on veut descendre bas en fréquence, plus il faut que la ligne soit de longueur importante. Notons cependant qu'un angle de 87 degrés (soit +- 43 degrés) confère une certaine directivité, et ce, dès 60 hz pour une ligne de 5 m de longueur.

L'objet de ce post est d'étudier la directivité d'une line array de 5 m de long composé de 6 HP, espacé d'un mètre.

Pour étudier la manière dont une line array distribue son énergie, on peut tracer le diagramme polaire de directivité. Voici un tel diagramme pour les fréquences 40 hz, 60 hz et 100 hz (les graduations sur l'axe radial sont espacées de 10 dB) :


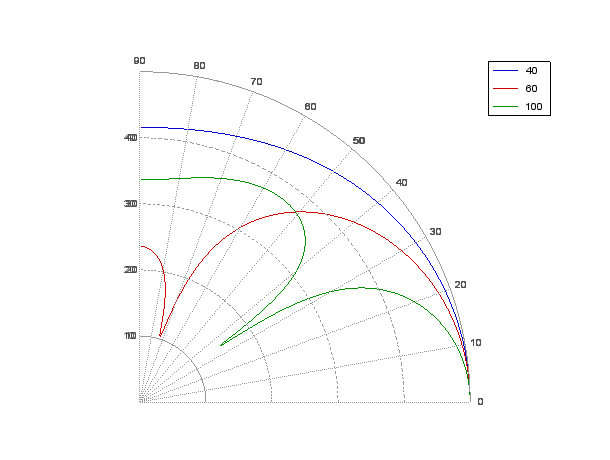
On constate l'apparition de lobes à partir de 60 hz. Pour les supprimer, on courbe la ligne, soit physiquement pour obtenir une ligne convexe, soit numériquement en retardant les enceintes aux extrémités. En prenant les délais suivants (ms) pour les 6 subs : 2,1,0,0,1,2 on obtient le diagramme suivant :


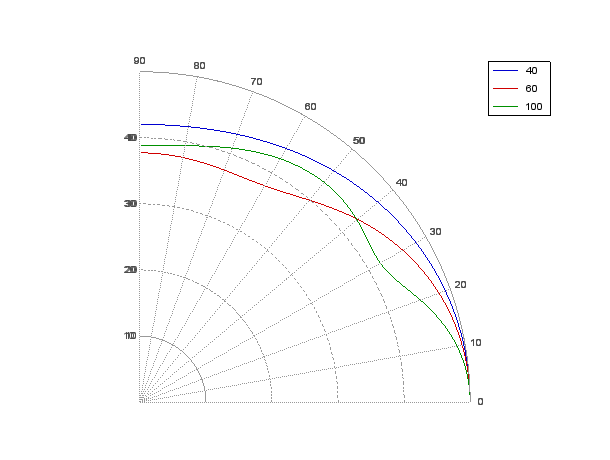
Notons que ces types de diagramme de directivité sont calculés à une distance largement supérieure à la largeur de la ligne pour que la directivité ne soit plus dépendante de la distance. Dans le cas qui nous intéresse, la ligne est écoutée à une distance de 4 m. De plus, à cette distance, les murs limitent l'angle de dispersion à environ +-37 degrés (la largeur de la salle est de 6m).

Si la technique de placement sur une ligne convexe, permet d'avoir un champ sonore plus homogène, il va à l'encontre de ce que l'on veut faire dans cette étude, à savoir augmenter la directivité. L'idée est donc de simuler une line array concave.

Pour quantifier le gain en termes de directivité, nous allons calculer le facteur de directivité Q et l'index de directivité. Les facteurs de directivité seront calculé en champ proche sur une sphère de rayon 4 m.

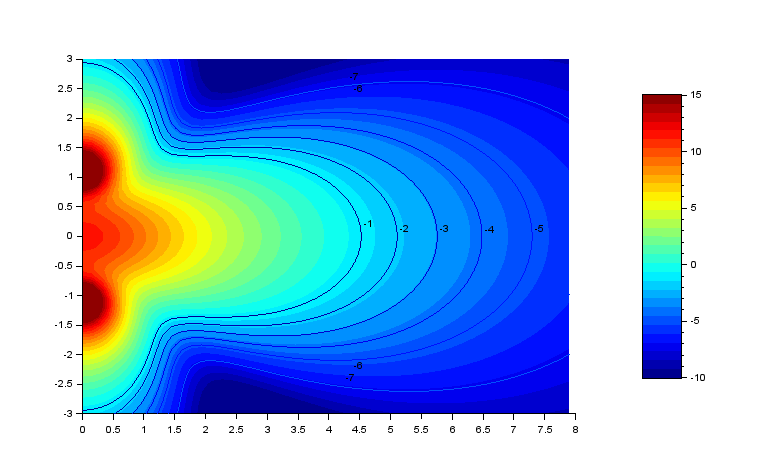
Pour avoir une idée précise de la manière dont la ligne rayonne, nous tracerons le champ sonore dans toute la surface de la salle en fixant le zéro dB à la position d'écoute. Nous comparerons la solution d'une line array avec celle de 2 sub espacés de 1.5 m. Notons que les diagrammes suivants représentent uniquement le champ direct et que dans cette étude, les murs sont censés avoir un coefficient d'absorption très important, et ce, très bas en fréquence.


Configuration 2 sub (espacement 1.5 m):

Voici ce que l'on obtient pour 40 hz, 60 hz et 100 hz :
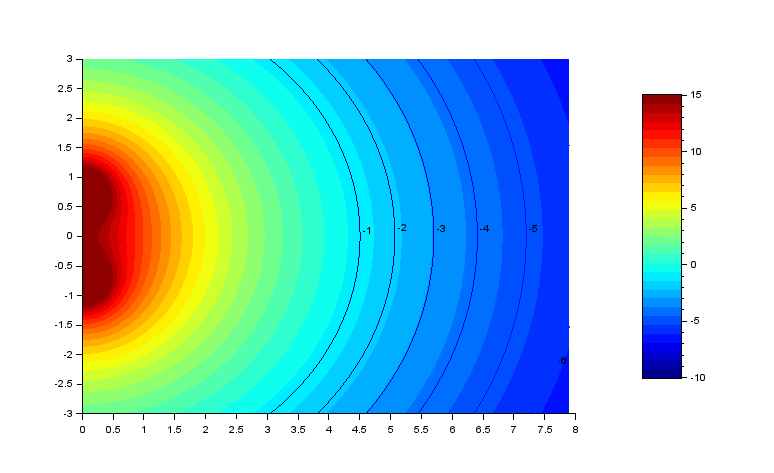
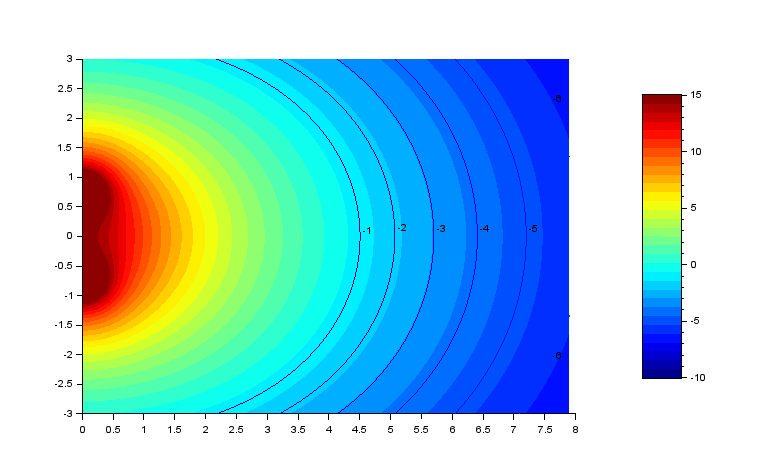
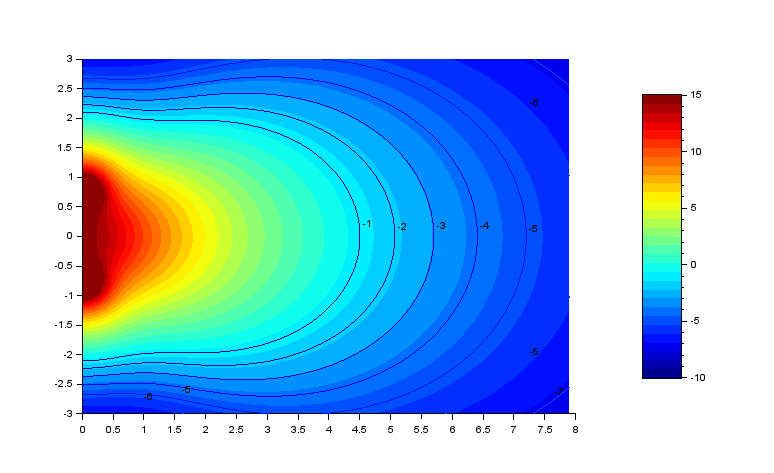Les facteurs de directivité sont :

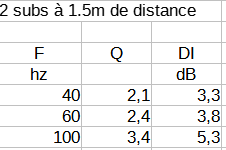
À 100 hz, le DI est donc de 5.3 dB à comparer à 3 dB d'une source purement hémisphérique.


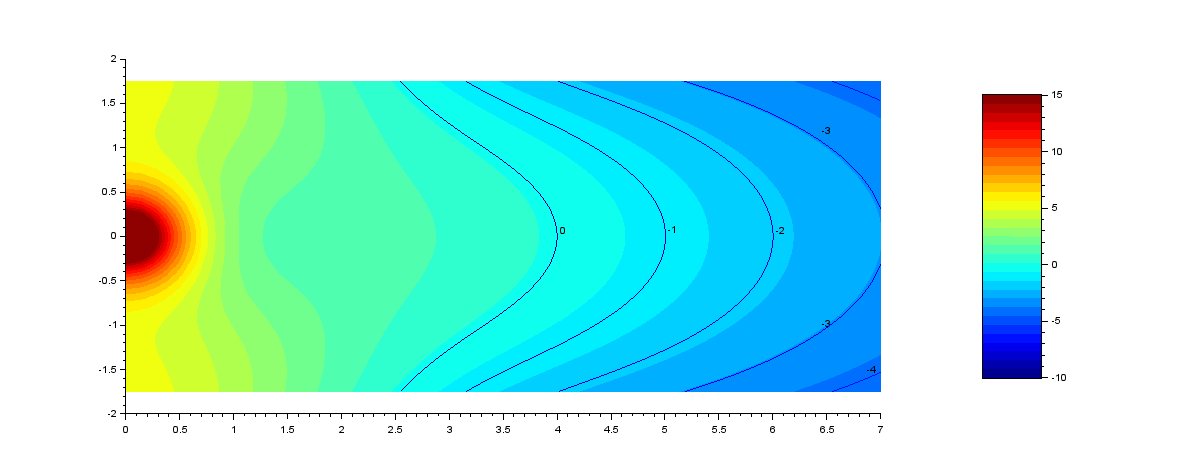
Line array droite :

Voici ce que l'on obtient pour 40 hz, 60 hz et 100 hz :
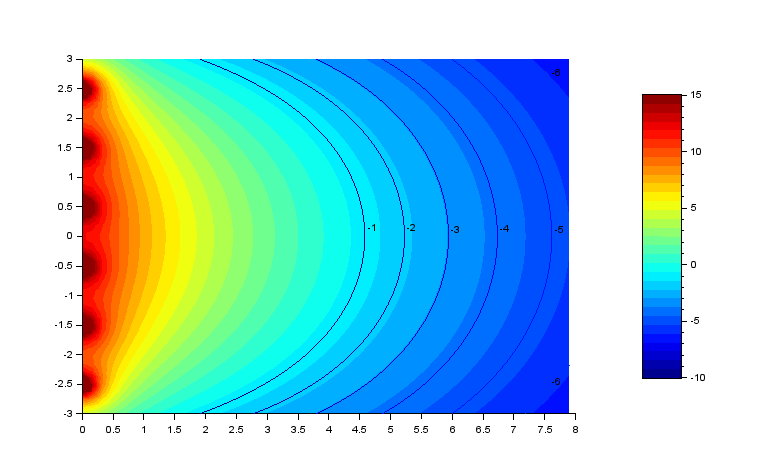
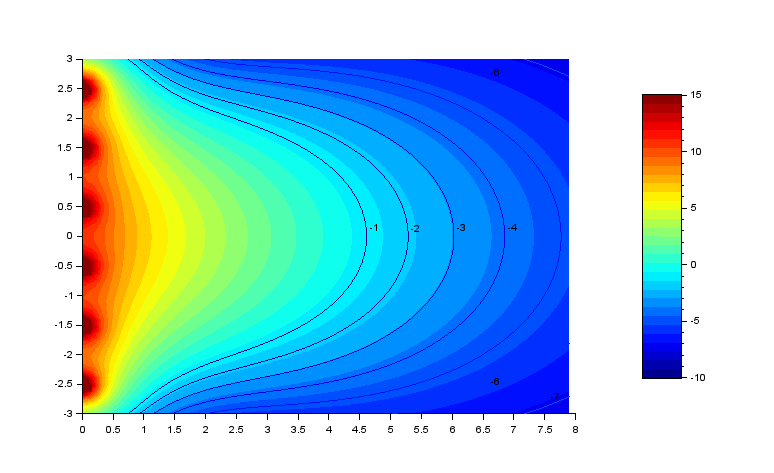
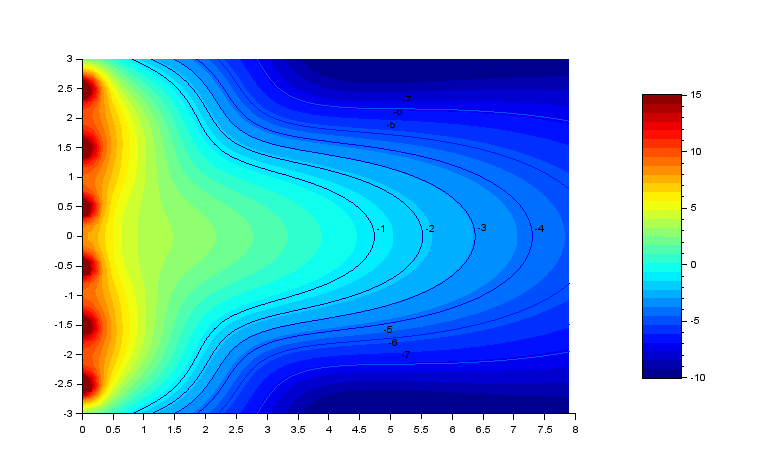Les facteur de directivité sont :

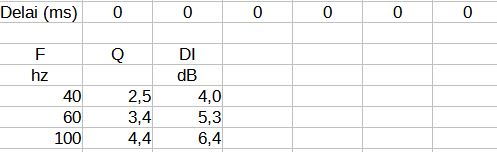
Cette configuration est un peu plus intéressante que celle avec 2 sub.


Line array convexe :

Si l'on courbe la ligne de manière convexe, on uniformise le champ sonore. Le voici pour une fréquence de 100 hz :
Mais les facteurs de directivité sont encore plus faible :


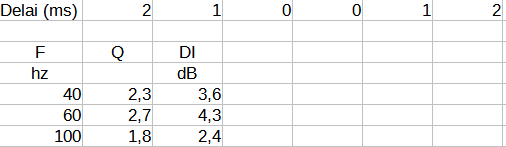
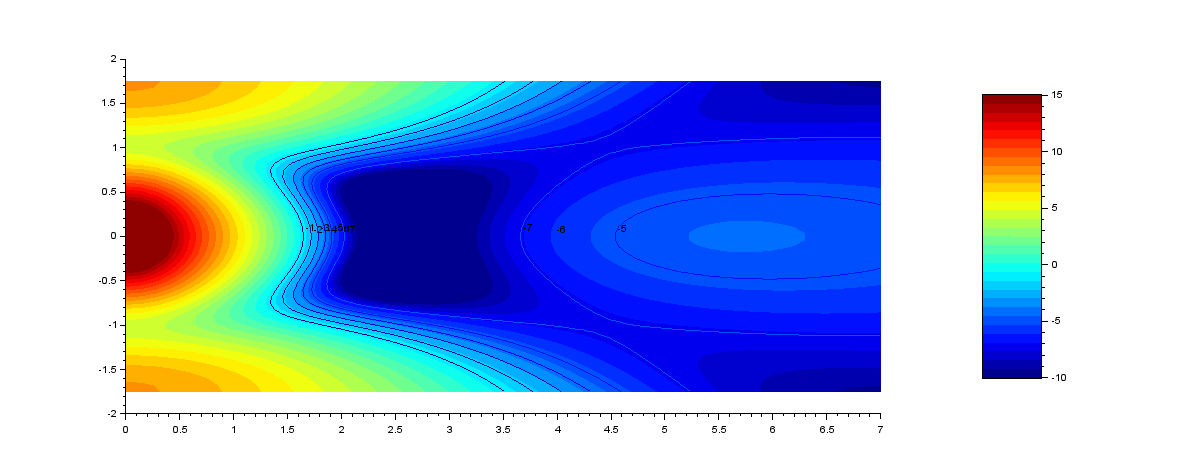
Line array concave:

Envisageons maintenant une line array concave avec les décalages temporels : 0 1.33 2.8 2.8 1.33 0

Voici le diagramme à 100 hz :


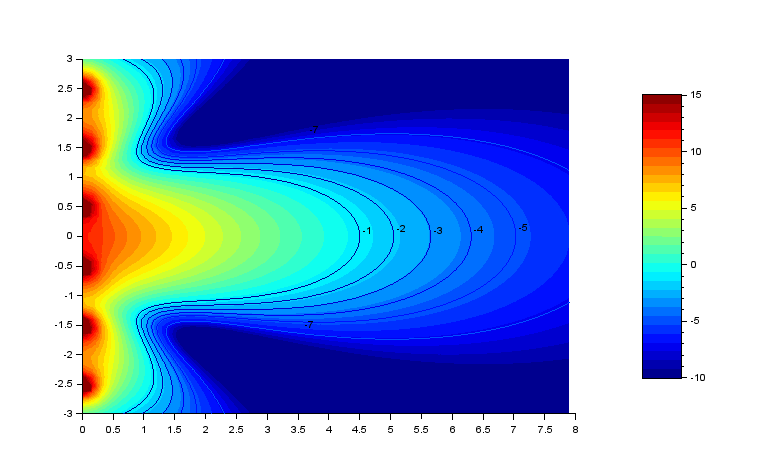
Et les facteurs de directivité :

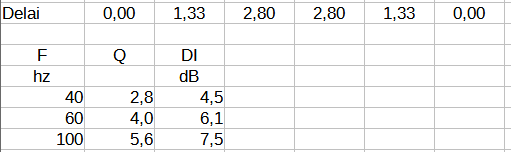
On obtient un gain de seulement 2,2 dB sur l'index de directivité par rapport à la solution 2 sub. Notons qu'en augmentant les délais, il y a apparition de lobes secondaires qui diminue le facteur de directivité.


Conclusion :

En terme de directivité, la solution d'une line array de 5 m n'offre pas de réel avantage. Quelque soit la longueur de la ligne, on ne peut pas gagner sur les deux tableaux : avoir une distribution homogène en largeur et un faible facteur de directivité.

Cordialement
Jean

Les sources des simulateurs : Line array Directivity Line array map

Un petit complément : si l'on cherche le facteur de directivité le plus élevé avec la configuration 2 sub, on trouve un écartement de 2.2 m qui donne à 100 hz, Q=4.5 et DI = 6.5 dB.

Voici le diagramme :
PS : j'ai corrigé le précédent message, certains tableaux des coefficients Q étaient inversés. Ca devrait être bon.

Parfaite demo Jean , instructive

Ouf ..impressionnant de boulot ..
Mais tu sais qu’il existe des softs constructeur tout fait et gratuit qui font tout cela
Avec cependant une grosse différence … il n’explique rien eux … ( joke)

Et en effet .. on ne peut gagner sur les 2 tableaux hélas .. ..
il faut donc limiter la largeur de bande d’usage .. et filtrer efficacement ..
Pour ma part avec la solution array je peut comparer toutes sortes de combinaison de HP
Puisque que chaque HP à son ampli et sa voie de processing

les simus c’est bien et même indispensable , mais les confirmer par l'écoute et la mesure c’est encore mieux ….( ce que j’ai fais lors de la construction de la salle avant de décider de la solution,.. )
J’ai essayé toutes les combinaisons frontales imaginables .. ..super simple :
Dans le LDP12 et avec 12 amplis ´ on fait la combinaison de HP . ( 2/ 4 / 7 … position que l’on veut , , le calage de volume pour comparer ã SPL identique / les délais de courbures ou pas / ect ..)et on met en mémoire .. ( 100 mémoires possibles )

Et ensuite on envoie la mesure
La bande d’usage est 10 / 55 hz pour le sub management et 10/ 110 hz pour le LFE ( en sachant que la bande LFE statistiquement ne contient pas grand chose voir rien au dessus de 70/80 hz )
Et clairement la plus avantageuse reste l’array .. :
variation de niveau suivant rangée bien plus cohérent avec le reste du spectre ( en théorie ..contraire à la logique ..mais la mesure est claire et l'écoute aussi )
Niveau général de grave baissant légèrement sur les fauteuils latéraux extrêmes des 3 rangés ( toutes les combinaisons standard donnant des montés importantes sur ces postions ..)
Niveau moyen de grave dans les angles arrières en baisse de plus de 15 dB par rapport aux combinaisons standards .
Linéarité dans la bande d’usage .. très supérieure aux combinaisons standards ( entre 10 et 50 hz ça tient dans 1,5 dB .sur 8 sièges de la rangėe 2 ( rangée principale )
5 dB sur la rangée 3 ( boost de 5 dB entre 10 et 20 hz !! donc on s’en fou)
6 dB sur la rangée 1 .. ( rangée quasi plein milieu longueur ..baisse en dessous de 19 hz .. )
Défaut : noch ultra étroit d’annulation venant du mur arrière ..à 18 et 21 , 5 hz .sur rangée 2 et 3 .. ( correspond pile au parcours d’onde aller/ retour ) ..n’existe que sur les fauteuils centraux
Noch totalement annulé par création d’un DBA entre 10 et 25 hz .. .

Le noch rear , avec les combinaisons «  non array » n’existe pas ( on suppose compensé par des réflexions latérales en sens inverses ) mais la réponse est évidemment beaucoup moins propre .. ( comme expliqué au dessus )
Comme tu le dit une combinaison array court( 5 m par exemple ) n’a pas d'interêt par rapport à une combinaison standard car entre autre la longueur de ligne ne permet pas un «  arrayage » sous 68 hz .. ..
La mesure confirme avec une réponse à distance non plate .. ..
La limite basse en guidage avec 11 m est vers 30 hz .. .. plus difficile de vérifier en salle ã ces fréquences .. mais parfaitement vérifié en externe .. ..
j’avais à l’époque testé une combinaison en 12 en montage «  onde plane » .. .. en dehors de l'impossibilité physique avec la présence des LCR .. 12 ne donnait pas un bon résultat , il en aurait fallu beaucoup plus ( ce n'était plus réaliste )
MP
Roland

Bonjour Roland,

Merci pour les informations complémentaires.

Oui, dans ton cas (salle de 11 m) de largeur, pas de doute : en théorie comme en pratique l'array est ce qui a de mieux.

Pour 6 mètre, 4 subs sur deux ligne (en SBA vertical) mais espacé latéralement de 2m me parait une très bonne solution. Ca laisse suffisamment de place pour ne pas coller les LR aux murs latéraux.

Oui .. nous sommes d’accord..
Car faut quand même penser que le plus important auditivement , spectralement et musicalement , justement ..c’est LR ..( ou LCR ) …
Et physiquement et pratiquement il existe toujours des contraintes et leurs positions est évidemment non «  négociable. »

Jean Fourcade a écrit : ↑05 oct. 2024, 15:11 Pour 6 mètre, 4 subs sur deux ligne (en SBA vertical) mais espacé latéralement de 2m me parait une très bonne solution. Ca laisse suffisamment de place pour ne pas coller les LR aux murs latéraux.

Hello,

Merci pour ces infos et détails ! impressionnant !

Je me permets une question alors : pourquoi 4 subs dans ce cas ? 2 espacés de 2 mètres ne font pas le même travail ? Peut être la capacité SPL ? Je dois raté un truc important :(

Bonjour,

Le principe du SBA (Single Bass Array, dont les simulations sont exposées par JIM dans ce post : viewtopic.php?t=126) est de placer suffisamment de HP verticalement et horizontalement pour générer une onde plane. On se sert pour cela de la réflexion de l'onde sur les murs latéraux, le plafond et le sol, ce qui crée des sources fantômes.

Une formule simple permet de calculer la limite haute en fréquence de ce fonctionnement qui est : f = C/(2H), avec C la vitesse du son et H l'espace entre les HP. Notons que pour qu'il y ait une source fantôme de rayonnement homogène avec les HP, il faut que les HP proches des parois soient positionnés à une distance H/2 de celles-ci. À partir de la formule ci-dessus, pour une largeur (ou hauteur) L d'une pièce donnée dans laquelle on place N HP, on déduit la fréquence limite : f = C N / (2L).

Dans mon cas, avec une hauteur de 3.5 m, si je place une seule ligne de HP (N=1), la fréquence limite est de 49 hz. Avec deux rangées, cette fréquence passe à 98 hz. Les sub devant être utilisé jusqu'à environ 80 hz, j'ai préféré cette solution avec deux lignes verticales de HP. Bien évidemment, il s'agit là d'une vision théorique qui se complique dans la pratique.

Dans le plan horizontal, je ne peux pas utiliser le principe du SBA, car je veux pouvoir décaler les LR du mur (notamment à cause du traitement acoustique qui fait 80 cm d'épaisseur). De plus, avec un mur frontal à pans coupés, le principe de fonctionnement d'une source fantôme ne fonctionne plus. J'ai donc opté pour resserrer les HP horizontalement comme expliqué dans ce post.

La raison d'utiliser 4 HP vient donc de la contrainte du SBA vertical et aussi, comme vous le précisez, de la capacité SPL.

Notons que je suis moins sensible aux modes latéraux que verticaux, car les deux murs ont un traitement acoustique alors que seul le plafond en a un.

Cordialement
Jean

Salut Jean,

Pour moi, le critère est plutôt f = C/(H) ou f = C N / (L).
Trinnov retient une valeur intermédiaire mais j'imagine que c'est plutôt pour prendre un peu de marge par rapport à la théorie. Il ne donne pas la formule mais fournissent une abaque (qui pousse un peu à la consommation de caissons).

En résonnant à l'ancienne uniquement avec l'aspect modal, ton premier mode vertical est à C/2L = 49 Hz
Le fait de positionner un caisson au centre (mi hauteur) annule l'effet des modes impairs. Le caisson est positionné dans le nœud des modes impairs.
Le premier mode à 49Hz n'est donc pas excité.

Les problèmes commenceront au second à 98Hz.
Tu as donc un peu de marge pour le raccord avec tes pavillons de grave.

Bonjour Jimmy,

La valeur de cette fréquence varie en fonction du critère que l'on se fixe et se situe entre C/2L et C/L. Si on résonne uniquement sur les mode, on tombe sur C/L comme tu l'expliques.

J'avais pris un critère plus restrictif qui est celui de la WST (line array) qui est que l'espacement entre les sub doit être la moitié de la longueur d'onde de la fréquence max, soit C/2L

Je ne suis pas étonné que Trinnov prenne une valeur intermédiaire entre les deux.

A la fréquence C/L, le niveau dans la pièce n'est quand même pas très homogène.

Avec les hypothèses suivantes : H=3.5m un seul HP au milieu de la hauteur, on a finalement 3 sources (dont deux fantômes) espacées de 3.5 m.

Voici le diagramme pour C/2H = 49 hz (j'ai calé le 0dB à 4m dans l'axe) :


Pour C/H = 98 hz (même puissance envoyée que dans le premier cas) :


A 4m dans l'axe, on a un trou de -6dB. Evidemment ces diagrammes ne sont que le champ direct. La vrai réponse est avec les modes et le champ réverbéré.

J'ai vu que Trinnov distribue gratuitement un logiciel pour positionner les subs. Il faudrait l'essayer.

PS : Tu t'es mis à utiliser Scilab ? C'est moins bien que Matlab, mais c'est gratuit !

En complément : comme expliqué, le choix de placement des sub dans mon cas est dicté par les contraintes géométriques.
Je ne peux pas faire de SBA horizontal (LR trop large 1,3m) et de plus avec un mur frontal à pan coupé, les réflexions latérales ne fonctionnement pas (pas de sources fantômes latérales).

De plus, au niveau SPL, 4 HP me parait un bon choix, d'où ma conf.

Difficile à prévoir dans tous les cas. J'avais raisonner sur l'aspect modal à partir d'une doc Harmann à l'époque.
Avec un SBA à 2 caissons sur la largeur, cela revient à positionner les caissons sur les noeuds du mode de rang 2.
J'avais vérifier la position de ces noeuds à la mesure avant de positionner les caissons mais j'avais comme toi la contrainte des enceintes LR. La position n'est pas juste à 10/20cm près de mémoire.

Avec le mur avant rigide, tu ne vas pas avoir beaucoup de souplesse.
Il serait peut être préférable de vérifier tout ça par la mesure avec le mur avant absorbant dans un premier temps, avant de monter le mur en dur.

Oui, le mur rigide est un problème. Une fois monté, plus possible de le déplacer. De même pour les pavillons si en dur.
Comment as-tu mesuré la position des nœuds ?

Un caisson contre la parois et mesure en sinus glissant côté opposé pour vérifier les fréquences des modes.
Dans un second temps, envoi d'un sinus pur sur le mode concerné pour rechercher sur l'axe le minimum de pression.

ps : Pas de besoin pour Scilab

Merci pour les précisions et informations !! Ok j'entre aperçois mieux le sujet.
J'essaye de noter dans un coin les ratios pour un usage futur (a new Hope)
(heu oui je n'ai pas grand chose à dire, à part merci pour les billes ... xD)