Identification des paramètres d'un BR
Posté : 04 mai 2024, 19:38
Bonjour à tous,
Je fais suite au message de Pascal présentant les mesures d'une enceinte BR avec un HP Faital 10RS430, c'est ici.
Pascal ayant communiqué les mesures, l'idée est de présenter une méthode d'identification des paramètres d'un BR à partir de la courbe d'impédance. J'en ai déjà parlé en donnant le lien d'un papier que j'ai écrit (voir ici) que je vais présenter de manière plus didactique.
Les paramètres du HP :
On connait tous les paramètres d'un HP qui sont :
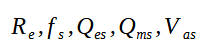
Ces paramètres vont être utilisés pour calculer un BR et simuler sa courbe de réponse. Un problème se pose toutefois concernant l'impédance de rayonnement qui peut ne pas être identique entre celle de la mesure et celle du HP monté dans l'enceinte.
L'impédance de rayonnement est la modélisation en terme électroacoustique de la pression de l'air sur la membrane. Ce terme se compose d'une partie réelle qui est un terme dissipatif qui modélise la conversion de l'énergie mécanique en énergie acoustique et un terme imaginaire assimilable à une masse. C'est la fameuse masse d'air qui vibre avec la membrane et qui a donc un effet sur la valeur de la fréquence de résonance et les facteurs de qualités puisque ceux-ci dépendent de la fréquence de résonance.
La valeur de cette masse dépend de la manière dont rayonne le HP. Sa valeur double si le HP est monté sur un écran inifni par rapport au même HP mesuré sans écran et où se produit un court-circuit acoustique. Cette variation est d'autant plus importante que la surface du HP est importante et la masse de son équipage mobile faible, ce qui est le cas du HP Altec qui équipe les enceintes Onken.
En toute rigueur, il faudrait donc utiliser pour simuler une enceinte BR les paramètres calculé avec la masse de rayonnement correspondante à l'enceinte. On notera ces paramètres, que l'on ne connait pas :
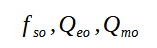
Les paramètres d'un BR :
Pour modéliser les paramètres d'un BR, on se donne de plus le volume net de l'enceinte et la fréquence de résonance de l'évent :
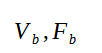
Pour simuler la réponse de l'enceinte, il faut prendre le volume apparent qui va dépendre du matériau acoustique placé contre les parois. Pour cela, on définit un paramètre beta qui est le facteur d'augmentation de compliance. On définit alors le 'tuning parameter" rapport entre la fréquence de résonance de l'évent et du haut-parleur et le facteur de compliance, rapport entre le volume d'air équivalent à la suspension du HP et le volume apparent de l'enceinte :
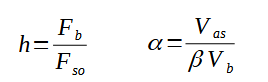
Il manque enfin pour simuler le BR les facteurs de pertes : Ql pertes par fuites d'air de l'enceinte, Qp pertes à travers l'event, Qa pertes par absorptions dans l'enceinte. On en déduit que le SPL est fonctions des paramètres suivants :
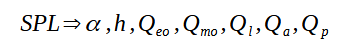
et l'impédance fonctions de ces mêmes paramètres auxquels if faut ajouter la résistance de la bobine mobile :
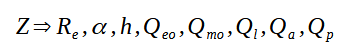
Comme on ne connait pas les paramètres du HP monté dans l'enceinte, on peut se poser la question : peut-on identifier tous ces paramètres à partir de la seule mesure d'impédance ?
Identification des paramètres d'un BR :
Les techniques d'identification font largement appel à la méthode dite des moindres carrés qui consiste à calculer un jeu de paramètres d'une fonction (ici l'impédance) dont on sait calculer la valeur théorique à partir de ce jeu de paramètres et des mesures de cette même fonction.
Pour la petite histoire, c'est le mathématicien Gauss qui a inventé la méthode des moindres carrés au début du 19ᵉ siècle pour déterminer la trajectoire de comètes…
Il existe une littérature mathématique considérable sur la technique des moindres carrés et notamment sur la manière de calculer la précision (écart type) de chaque paramètre restitué.
En tentant d'appliquer cette méthode au problème qui nous intéresse, on constate que les paramètres peuvent se classer en trois catégories : les paramètres inobservables (Qmo, Ql, Qa, Qp) les paramètres observables mais corrélés aux précédents (h et alpha) et les paramètres parfaitement identifiables (fso, Qeo).
Dire que les paramètres Qmo, Ql, Qa, Qp sont inobservables en mesurant l'impédance signifie qu'il existe une infinité de combinaisons de ces paramètres donnant strictement la même courbe d'impédance.
Pour résoudre le porblème, il nous faut donc trouver un moyen de calculer la valeur de Qmo en dehors de la mesure d'impédance. Pour cela, l'idée est de se servir de la mesures des paramètres du HP seul.
On introduit à cette fin un paramètre "q" que l'on définit comme le rapport de la masse de rayonnement du HP mesuré seul à celui de ce même HP mesuré dans l'enceinte. Ce paramètres "q" permet de lier les paramètres Fs, Qes, Qms et Fso, Qeo et Qmo par les relations :
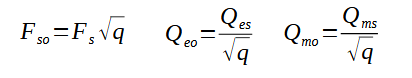
Connaissant les paramètres Fs, Qes, Qms, le problème d'identification des paramètres d'un BR revient alros à identifier :
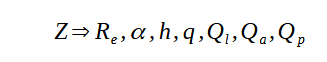
Cette identification est possible et pour être précise doit se baser sur les mesures simultanées du module et de la phase de l'impédance.
Application au 10RS430 :
A partir de la mesure de l'impédance du HP seul, on identifie par moindres carrés les paramètres du HP. Voici les courbes d'identification :
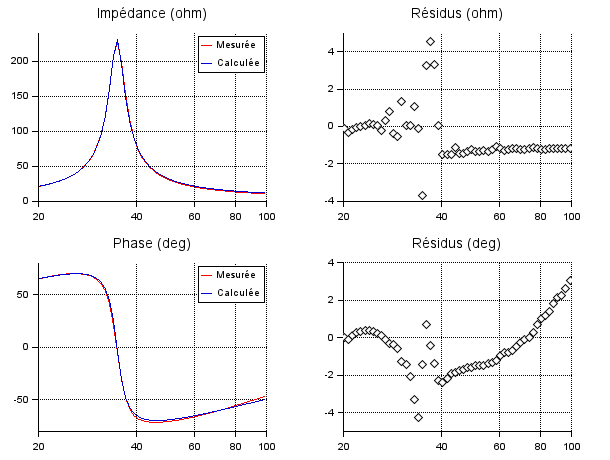
Sur les courbes de gauche, nous avons en rouge l'impédance mesurée et en bleu l'impédance calculée. Les courbes de droites donnent ce qu'on appelle les résidus, c'est-à-dire les écarts entre les mesures théoriques et les mesures réelles.
Cette identification conduit aux paramètres du HP suivants :
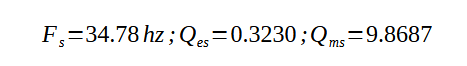
On peut alors identifier les paramètres du BR. Voici avec les mêmes conventions les courbes d'idntifications :
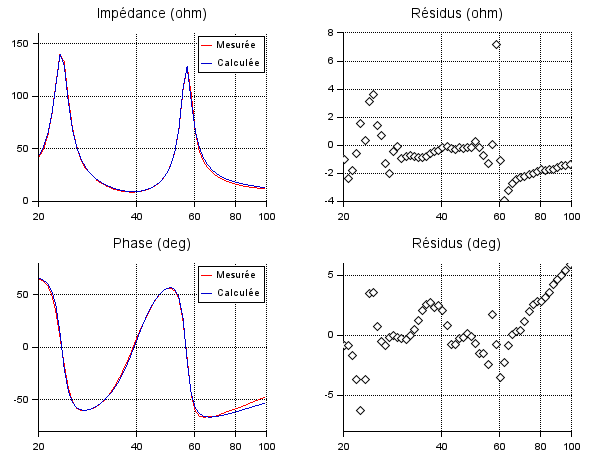Ces courbes conduisent aux paramètres suivants :
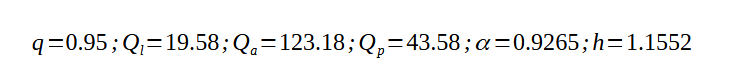
On remarque la valeur du paramètre q qui vaut 0.95 (ce qui correspond à une variation de 3% de la fréquence de résonance). Dans le cas d'un HP comme l'Altec 416, on trouve une valeur de q de 0.9 (ce qui correspond à une variation de 6% de la fréquence de résonance).
On identifie également les valeurs des pertes Ql,Qa,Qp supérieures à 10 signe d'une enceinte correctement réalisée.
En prenant comme valeur de Vas celle du constructeur soit 61.5 l et un volume net de l'enceinte de 50l, on en déduit le facteur d'augmentation de compliance, le volume apparent et la fréquence d'accord :
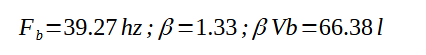
On peut alors simuler la courbe de réponse à l'aide de WinISD en entrant les paramètres identifiés :
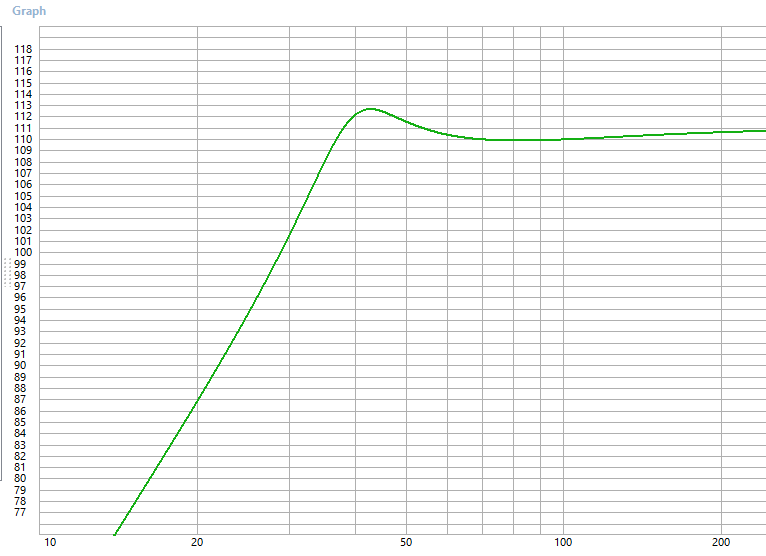
Pour aller plus loin, Pascal, on peut mesurer la courbe de réponse en plaçant un microphone dans l'enceinte (méthode MIB) et la comparer à la courbe ci-dessus.
Cordialement
Jean
Je fais suite au message de Pascal présentant les mesures d'une enceinte BR avec un HP Faital 10RS430, c'est ici.
Pascal ayant communiqué les mesures, l'idée est de présenter une méthode d'identification des paramètres d'un BR à partir de la courbe d'impédance. J'en ai déjà parlé en donnant le lien d'un papier que j'ai écrit (voir ici) que je vais présenter de manière plus didactique.
Les paramètres du HP :
On connait tous les paramètres d'un HP qui sont :
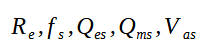
Ces paramètres vont être utilisés pour calculer un BR et simuler sa courbe de réponse. Un problème se pose toutefois concernant l'impédance de rayonnement qui peut ne pas être identique entre celle de la mesure et celle du HP monté dans l'enceinte.
L'impédance de rayonnement est la modélisation en terme électroacoustique de la pression de l'air sur la membrane. Ce terme se compose d'une partie réelle qui est un terme dissipatif qui modélise la conversion de l'énergie mécanique en énergie acoustique et un terme imaginaire assimilable à une masse. C'est la fameuse masse d'air qui vibre avec la membrane et qui a donc un effet sur la valeur de la fréquence de résonance et les facteurs de qualités puisque ceux-ci dépendent de la fréquence de résonance.
La valeur de cette masse dépend de la manière dont rayonne le HP. Sa valeur double si le HP est monté sur un écran inifni par rapport au même HP mesuré sans écran et où se produit un court-circuit acoustique. Cette variation est d'autant plus importante que la surface du HP est importante et la masse de son équipage mobile faible, ce qui est le cas du HP Altec qui équipe les enceintes Onken.
En toute rigueur, il faudrait donc utiliser pour simuler une enceinte BR les paramètres calculé avec la masse de rayonnement correspondante à l'enceinte. On notera ces paramètres, que l'on ne connait pas :
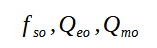
Les paramètres d'un BR :
Pour modéliser les paramètres d'un BR, on se donne de plus le volume net de l'enceinte et la fréquence de résonance de l'évent :
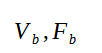
Pour simuler la réponse de l'enceinte, il faut prendre le volume apparent qui va dépendre du matériau acoustique placé contre les parois. Pour cela, on définit un paramètre beta qui est le facteur d'augmentation de compliance. On définit alors le 'tuning parameter" rapport entre la fréquence de résonance de l'évent et du haut-parleur et le facteur de compliance, rapport entre le volume d'air équivalent à la suspension du HP et le volume apparent de l'enceinte :
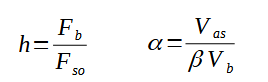
Il manque enfin pour simuler le BR les facteurs de pertes : Ql pertes par fuites d'air de l'enceinte, Qp pertes à travers l'event, Qa pertes par absorptions dans l'enceinte. On en déduit que le SPL est fonctions des paramètres suivants :
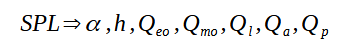
et l'impédance fonctions de ces mêmes paramètres auxquels if faut ajouter la résistance de la bobine mobile :
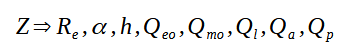
Comme on ne connait pas les paramètres du HP monté dans l'enceinte, on peut se poser la question : peut-on identifier tous ces paramètres à partir de la seule mesure d'impédance ?
Identification des paramètres d'un BR :
Les techniques d'identification font largement appel à la méthode dite des moindres carrés qui consiste à calculer un jeu de paramètres d'une fonction (ici l'impédance) dont on sait calculer la valeur théorique à partir de ce jeu de paramètres et des mesures de cette même fonction.
Pour la petite histoire, c'est le mathématicien Gauss qui a inventé la méthode des moindres carrés au début du 19ᵉ siècle pour déterminer la trajectoire de comètes…
Il existe une littérature mathématique considérable sur la technique des moindres carrés et notamment sur la manière de calculer la précision (écart type) de chaque paramètre restitué.
En tentant d'appliquer cette méthode au problème qui nous intéresse, on constate que les paramètres peuvent se classer en trois catégories : les paramètres inobservables (Qmo, Ql, Qa, Qp) les paramètres observables mais corrélés aux précédents (h et alpha) et les paramètres parfaitement identifiables (fso, Qeo).
Dire que les paramètres Qmo, Ql, Qa, Qp sont inobservables en mesurant l'impédance signifie qu'il existe une infinité de combinaisons de ces paramètres donnant strictement la même courbe d'impédance.
Pour résoudre le porblème, il nous faut donc trouver un moyen de calculer la valeur de Qmo en dehors de la mesure d'impédance. Pour cela, l'idée est de se servir de la mesures des paramètres du HP seul.
On introduit à cette fin un paramètre "q" que l'on définit comme le rapport de la masse de rayonnement du HP mesuré seul à celui de ce même HP mesuré dans l'enceinte. Ce paramètres "q" permet de lier les paramètres Fs, Qes, Qms et Fso, Qeo et Qmo par les relations :
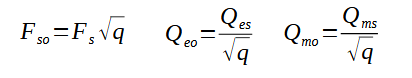
Connaissant les paramètres Fs, Qes, Qms, le problème d'identification des paramètres d'un BR revient alros à identifier :
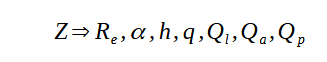
Cette identification est possible et pour être précise doit se baser sur les mesures simultanées du module et de la phase de l'impédance.
Application au 10RS430 :
A partir de la mesure de l'impédance du HP seul, on identifie par moindres carrés les paramètres du HP. Voici les courbes d'identification :
Sur les courbes de gauche, nous avons en rouge l'impédance mesurée et en bleu l'impédance calculée. Les courbes de droites donnent ce qu'on appelle les résidus, c'est-à-dire les écarts entre les mesures théoriques et les mesures réelles.
Cette identification conduit aux paramètres du HP suivants :
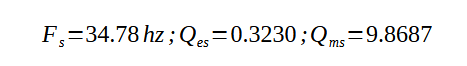
On peut alors identifier les paramètres du BR. Voici avec les mêmes conventions les courbes d'idntifications :
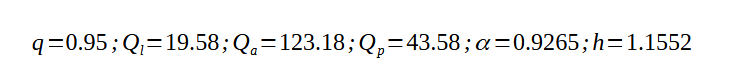
On remarque la valeur du paramètre q qui vaut 0.95 (ce qui correspond à une variation de 3% de la fréquence de résonance). Dans le cas d'un HP comme l'Altec 416, on trouve une valeur de q de 0.9 (ce qui correspond à une variation de 6% de la fréquence de résonance).
On identifie également les valeurs des pertes Ql,Qa,Qp supérieures à 10 signe d'une enceinte correctement réalisée.
En prenant comme valeur de Vas celle du constructeur soit 61.5 l et un volume net de l'enceinte de 50l, on en déduit le facteur d'augmentation de compliance, le volume apparent et la fréquence d'accord :
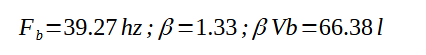
On peut alors simuler la courbe de réponse à l'aide de WinISD en entrant les paramètres identifiés :
Pour aller plus loin, Pascal, on peut mesurer la courbe de réponse en plaçant un microphone dans l'enceinte (méthode MIB) et la comparer à la courbe ci-dessus.
Cordialement
Jean
