Bonjour à tous,
Pour aller un peu plus loin dans ces échanges, on peut essayer de simuler le pavillon donné par Sensunda.
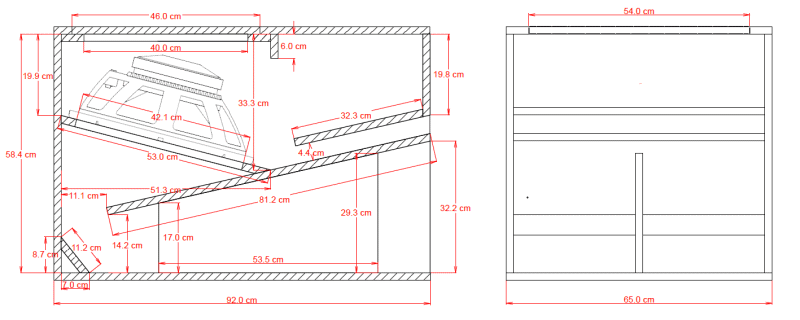
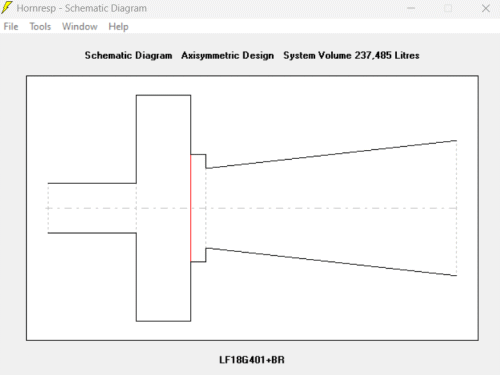
Voici le schéma :
Il s'agit d'un pavillon frontal monté sur un 18", le RCF LF18G401 dont les paramètres sont : Sd = 1220 cm2, Fs=33 hz, Re=4.8 Ohm, Vas=268 l, Qes=0.3, Qms=7.6. Le HP est monté dans un BR dont l'évent rayonne sur la même face que le pavillon. Le schéma montre qu'il s'agit d'un pavillon conique.
Il est intéressant d'ouvrir une parenthèse concernant les caractéristiques des pavillons. On sait que les pavillons ont une fréquence de coupure qui est la fréquence en dessous de laquelle l'impédance de gorge est purement réactive, ce qui signifie que le pavillon ne transmet plus de puissance acoustique (l'impédance résistive de rayonnement est nulle).
En réalité, cette fréquence n'est pas la fréquence de coupure de l'ensemble HP + pavillon qui se définit (comme toute fréquence de coupure) comme étant la fréquence à demi puissance. Cette fréquence est nécessairement plus élevée que la fréquence de coupure du pavillon.
Un pavillon conique est dénué de fréquence de coupure proprement dite, car l'impédance résistive de rayonnement ne devient jamais nulle. Ce n'est pas pour autant qu'un pavillon conique n'a pas de fréquence de coupure calculée classiquement à -3 dB.
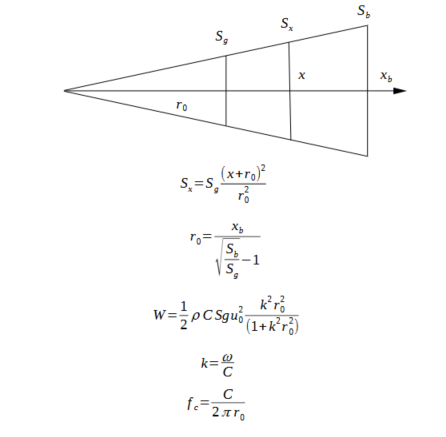
Le schéma suivant montre un pavillon conique en coupe et donne quelques formules associées :
Le paramètre r0 est la distance de la surface de la gorge par rapport à l'origine zéro de l'axe x. On en déduit la formule d'expansion de surface Sx en fonction de x, la distance par rapport à la gorge.
Connaissant la surface de gorge, la surface de bouche et la distance entre la gorge et la bouche, on peut calculer le paramètre r0.
À partir du schéma du pavillon étudié, on déduit : Sg = 111 mm x 600 mm ; Sb = 322 mm x 600 mm et la distance entre la bouche et la gorge : 920 mm. On en déduit r0 = 1,31 m.
La puissance acoustique émise par un pavillon conique est donnée par l'expression W dans laquelle C est la vitesse du son, ρ la densité de l'air, u0 la vitesse des particule d'air, et k le nombre d'onde (ω/C).
A partir de cette équation on peut calculer la fréquence de coupure du pavillon conique à mi- puissance fc. On constate le rôle important que joue le paramètre k0 puisqu'il permet de calculer la fréquence de coupure du pavillon. Avec r0=1,31 m, on trouve fc=42 hz. Le pavillon a donc bien été calculé pour une fréquence de coupure de l'ensemble autour de 40 hz.
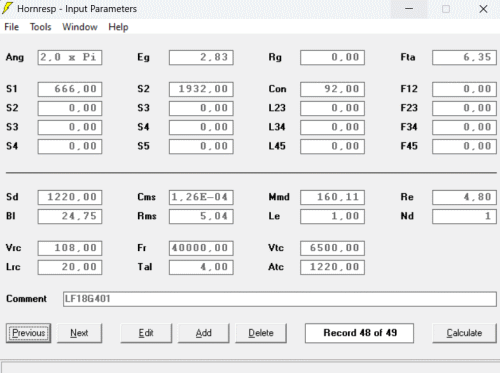
Pour aller plus loin, il faut simuler la réponse avec HornResp. Simulons dans un premier temps le pavillon avec le HP monté dans une enceinte close. J'ai pris comme volume de cette enceinte : 108 litres. Voici ce que donne la simulation :
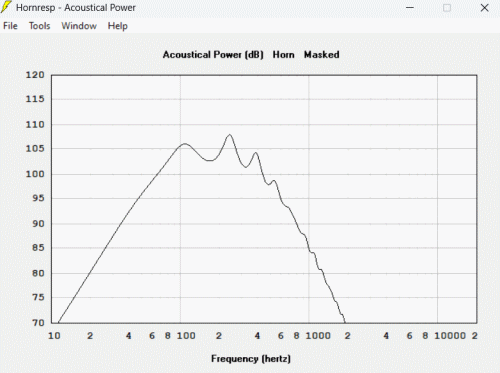
Et voici la courbe de réponse :
La fréquence ce coupure n'est pas de 40 hz car le pavillon est bien trop court pour cette fréquence, la surface de bouche étant trop petite.
Simulons maintenant le pavillon avec le HP monté en BR. J'ai pris comme surface d'évent : 4,4 cm x 60 cm = 264 cm2 (paramètre Ap) et comme longueur d'évent 32,3 cm (paramètre Lpt)
Voici le schéma du pavillon :
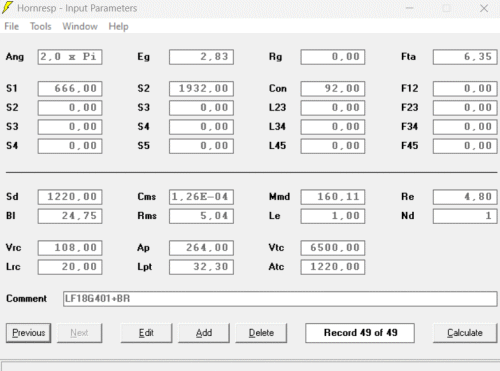
Les paramètres dans HonResp ;
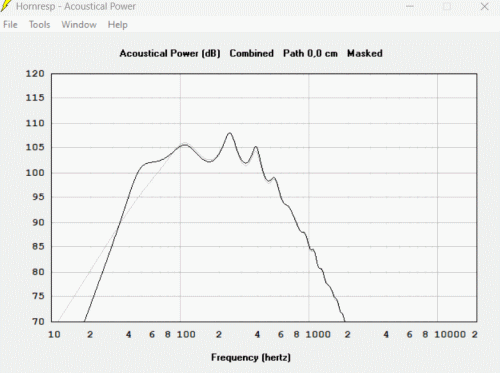
et la courbe de réponse (en noir montage avec le BR, en gris en enceinte close avec seulement le pavillon qui rayonne) :
On obtient la courbe de réponse typique de ce genre de montage, un réponse non linéaire avec une remonté de puissance lorsque le pavillon devient efficace et des oscillations dans la bande du fait d'un pavillon trop court.
Cordialement
Jean