Les pavillons coniques
Posté : 23 sept. 2025, 15:11
Bonjour à tous,
On m'a interrogé au sujet de l'utilisation de pavillons coniques. La réponse pouvant intéresser d'autres personnes, j'ouvre ce post. Ce sera également l'occasion d'évoquer les pavillons atypiques Synergy Horn.
On sait que les pavillons ont une fréquence de coupure qui dépend de la loi d'expansion. Cependant, les pavillons coniques n'ont pas de fréquence de coupure. De plus ils ont une directivité constante y compris bas en fréquence. Ils semblent donc n'avoir que des avantages. Dès lors, pourquoi ceux-ci ne sont-ils pas plus utilisés ?
La fréquence de coupure d'un pavillon est la fréquence à laquelle la résistance de rayonnement est nulle. En dessous de cette fréquence, le pavillon ne transmet plus d'énergie sonore.
Mais, de même que pour tout système d'entrée-sortie, on peut définir pour un pavillon une fréquence de coupure effective f3 qui est la fréquence à laquelle la puissance dissipée est divisée par deux. Cette fréquence f3 diffère de la fréquence de coupure proprement dite du pavillon. La puissance dissipée étant proportionnelle à la résistance de la gorge, la fréquence f3 est donc la fréquence à laquelle la résistance de gorge normalisée vaut 1/2.
Le graphique suivant (d'Olson en 1947, mais toujours d'actualité...) montre la résistance et la réactance acoustique normalisée de différents pavillons de longueur infini (conique, exponentiel, hyperbolique et cylindrique) ayant la même surface de gorge et la même surface de bouche à 1 m (sauf évidemment pour le pavillon cylindrique dont la surface est constante) :
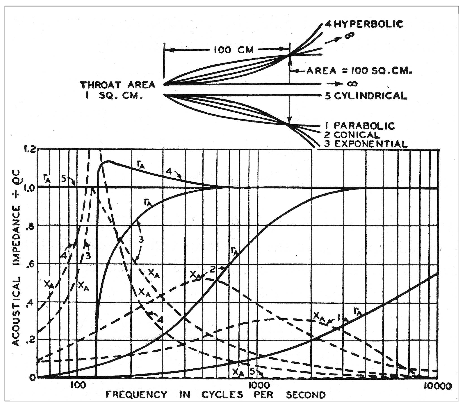
On remarque que le pavillon cylindrique a une réactance nulle et une résistance constance jusqu'à la fréquence nulle. Ce pavillon est donc idéal pour étudier la réponse des chambres de compression.
Ce graphique montre de plus que les pavillons exponentiels et hyperboliques ont, pour les dimensions choisies, une fréquence de coupure située autour de 130 Hz. On constate que le pavillon conique a bien une fréquence de coupure nulle, puisque la résistance de rayonnement n'est nulle qu'à cette fréquence.
Cependant, si l'on mesure sur cette figure la fréquence f3 du pavillon conique, celle-ci est autour de 500 Hz. Ainsi, bien que le pavillon conique n'ait pas de fréquence de coupure, sa fréquence f3 est largement supérieure à celle des pavillons hyperbolique ou exponentiel. De plus la forme de la résistance de rayonnement (la coupure n'est pas franche) montre que le pavillon charge mal la membrane.
On peut montrer que la puissance dissipée par un pavillon conique est de la forme :
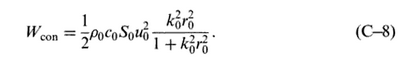
Dans cette formule, S0 est la surface de la gorge, u0 est la vitesse de l'air au niveau de la gorge (constante dans un pavillon), k0 le nombre d'onde (pulsation divisée par la vitesse du son). Ko est un coefficient qui caractérise l'angle d'ouverture du pavillon défini suivant le schéma suivant :
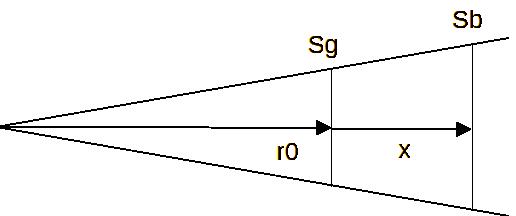
De la formule ci-dessus, on calcule la fréquence à laquelle la puissance W est divisée par deux et on obtient la fréquence de coupure f3 du pavillon conique donnée par :
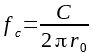
Le fichier Excel suivant calcule cette formule : Impédance gorge
En reprenant l'exemple d'Olson (1cm2 de gorge, 100 cm2 de bouche à 1m), on trouve r0 = 11,11 cm soit une valeur de f3 de 492 hz.
Cette formule est théorique. La forme de la résistance de rayonnement ayant une faible pente, la coupure ne sera pas franche et se traduira surtout par des oscillations de la réponse dans la bande reproduite.
Cependant, la formule ci-dessus conduit à une importante conclusion qui est utilisée dans les pavillons Synergy Horn.
La fréquence de coupure d'un pavillon hyperbolique dépend de la forme de l'expansion (plus ou moins rapide) mais est indépendante de la surface de la bouche (Édit : gorge et non bouche)
Il n'en est pas de même d'un pavillon conique. La formule de la fréquence f3 du pavillon conique montre que celle-ci est inversement proportionnelle au paramètre r0 (distance entre l'apex et la gorge). On en déduit que pour un même cône (même angle d'ouverture), plus on placera la source émissive (gorge) loin de l'apex, plus r0 augmentera et plus la fréquence de coupure diminuera.
On peut expliquer ce phénomène par le raisonnement suivant :
Un pavillons hyperboliques voit sa surface doublé pour une distance donnée dépendant de la fréquence de coupure. Plus la fréquence de coupure est basse plus cette distance est importante. Mais quelles que soient les sections prises en comptes le long du pavillon, cette distance reste la même.
Il n'en est pas de même d'un pavillon conique. L'expansion d'un pavillon conique est très rapide proche de la gorge et croît plus lentement au fur et à mesure que l'on s'éloigne de l'apex. Il en résulte une variation de la loi d'expansion le long de l'axe du pavillon et une différence de fréquence de coupure.
Cet effet permet de placer plusieurs transducteurs le long d'un pavillon conique comme le montre le schéma ci-dessous (Synergy horn) :
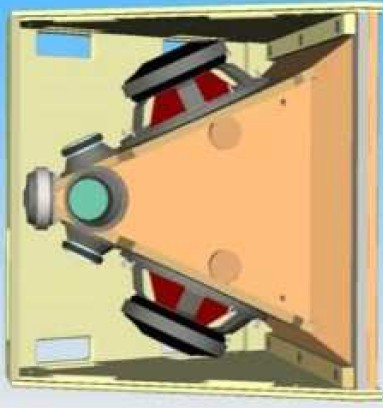
De fait, les membranes de chaque haut-parleur se trouvent correctement chargées. Voici le lien sur un article théorique concernant ces pavillons : Sysnergy Horn Technologies
Pour terminer, une petite vidéo de démonstration de la directivité d'un pavillon : SH-50 (je ne suis pas sûr que le microphone se déplace bien le long d'un cercle centré sur l'apex .. mais bon )
)
Cordialement
Jean
On m'a interrogé au sujet de l'utilisation de pavillons coniques. La réponse pouvant intéresser d'autres personnes, j'ouvre ce post. Ce sera également l'occasion d'évoquer les pavillons atypiques Synergy Horn.
On sait que les pavillons ont une fréquence de coupure qui dépend de la loi d'expansion. Cependant, les pavillons coniques n'ont pas de fréquence de coupure. De plus ils ont une directivité constante y compris bas en fréquence. Ils semblent donc n'avoir que des avantages. Dès lors, pourquoi ceux-ci ne sont-ils pas plus utilisés ?
La fréquence de coupure d'un pavillon est la fréquence à laquelle la résistance de rayonnement est nulle. En dessous de cette fréquence, le pavillon ne transmet plus d'énergie sonore.
Mais, de même que pour tout système d'entrée-sortie, on peut définir pour un pavillon une fréquence de coupure effective f3 qui est la fréquence à laquelle la puissance dissipée est divisée par deux. Cette fréquence f3 diffère de la fréquence de coupure proprement dite du pavillon. La puissance dissipée étant proportionnelle à la résistance de la gorge, la fréquence f3 est donc la fréquence à laquelle la résistance de gorge normalisée vaut 1/2.
Le graphique suivant (d'Olson en 1947, mais toujours d'actualité...) montre la résistance et la réactance acoustique normalisée de différents pavillons de longueur infini (conique, exponentiel, hyperbolique et cylindrique) ayant la même surface de gorge et la même surface de bouche à 1 m (sauf évidemment pour le pavillon cylindrique dont la surface est constante) :

On remarque que le pavillon cylindrique a une réactance nulle et une résistance constance jusqu'à la fréquence nulle. Ce pavillon est donc idéal pour étudier la réponse des chambres de compression.
Ce graphique montre de plus que les pavillons exponentiels et hyperboliques ont, pour les dimensions choisies, une fréquence de coupure située autour de 130 Hz. On constate que le pavillon conique a bien une fréquence de coupure nulle, puisque la résistance de rayonnement n'est nulle qu'à cette fréquence.
Cependant, si l'on mesure sur cette figure la fréquence f3 du pavillon conique, celle-ci est autour de 500 Hz. Ainsi, bien que le pavillon conique n'ait pas de fréquence de coupure, sa fréquence f3 est largement supérieure à celle des pavillons hyperbolique ou exponentiel. De plus la forme de la résistance de rayonnement (la coupure n'est pas franche) montre que le pavillon charge mal la membrane.
On peut montrer que la puissance dissipée par un pavillon conique est de la forme :
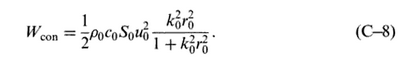
Dans cette formule, S0 est la surface de la gorge, u0 est la vitesse de l'air au niveau de la gorge (constante dans un pavillon), k0 le nombre d'onde (pulsation divisée par la vitesse du son). Ko est un coefficient qui caractérise l'angle d'ouverture du pavillon défini suivant le schéma suivant :

De la formule ci-dessus, on calcule la fréquence à laquelle la puissance W est divisée par deux et on obtient la fréquence de coupure f3 du pavillon conique donnée par :
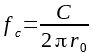
Le fichier Excel suivant calcule cette formule : Impédance gorge
En reprenant l'exemple d'Olson (1cm2 de gorge, 100 cm2 de bouche à 1m), on trouve r0 = 11,11 cm soit une valeur de f3 de 492 hz.
Cette formule est théorique. La forme de la résistance de rayonnement ayant une faible pente, la coupure ne sera pas franche et se traduira surtout par des oscillations de la réponse dans la bande reproduite.
Cependant, la formule ci-dessus conduit à une importante conclusion qui est utilisée dans les pavillons Synergy Horn.
La fréquence de coupure d'un pavillon hyperbolique dépend de la forme de l'expansion (plus ou moins rapide) mais est indépendante de la surface de la bouche (Édit : gorge et non bouche)
Il n'en est pas de même d'un pavillon conique. La formule de la fréquence f3 du pavillon conique montre que celle-ci est inversement proportionnelle au paramètre r0 (distance entre l'apex et la gorge). On en déduit que pour un même cône (même angle d'ouverture), plus on placera la source émissive (gorge) loin de l'apex, plus r0 augmentera et plus la fréquence de coupure diminuera.
On peut expliquer ce phénomène par le raisonnement suivant :
Un pavillons hyperboliques voit sa surface doublé pour une distance donnée dépendant de la fréquence de coupure. Plus la fréquence de coupure est basse plus cette distance est importante. Mais quelles que soient les sections prises en comptes le long du pavillon, cette distance reste la même.
Il n'en est pas de même d'un pavillon conique. L'expansion d'un pavillon conique est très rapide proche de la gorge et croît plus lentement au fur et à mesure que l'on s'éloigne de l'apex. Il en résulte une variation de la loi d'expansion le long de l'axe du pavillon et une différence de fréquence de coupure.
Cet effet permet de placer plusieurs transducteurs le long d'un pavillon conique comme le montre le schéma ci-dessous (Synergy horn) :

De fait, les membranes de chaque haut-parleur se trouvent correctement chargées. Voici le lien sur un article théorique concernant ces pavillons : Sysnergy Horn Technologies
Pour terminer, une petite vidéo de démonstration de la directivité d'un pavillon : SH-50 (je ne suis pas sûr que le microphone se déplace bien le long d'un cercle centré sur l'apex .. mais bon
Cordialement
Jean