Le problème des modes en basse fréquence
Posté : 17 sept. 2024, 11:52
Bonjour à tous,
On sait tous qu'un des problèmes majeurs en acoustique concerne le traitement des modes en basses fréquences. Ces modes dépendent fortement de la géométrie de la pièce et de ses dimensions.
L'idéal serait d'être dénué de tout régime modal. On connait la fréquence de Schröder qui fixe la limite entre le régime diffus et le régime modal. Cette fréquence peut-elle être suffisamment basse pour éviter un traitement acoustique lourd dans les basses fréquences ?
L'objet de ce post est d'aborder le problème des modes en basses fréquences et de quantifier l'importance de la taille de la salle.
Le calcul du temps de réverbération, formules de Sabine :
Rappelons quelques formules concernant le calcul du temps de réverbération selon la formulation de Sabine. Nous avons :
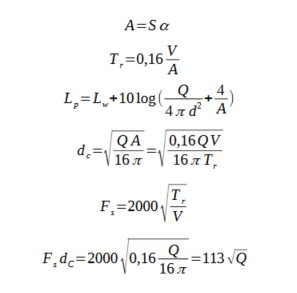 La salle se caractérise par un volume V, une surface des parois S et une aire d'absorption acoustique A. On note α le coefficient d'absorption moyen de la salle. On en déduit le temps de réverbération de la salle Tr.
La salle se caractérise par un volume V, une surface des parois S et une aire d'absorption acoustique A. On note α le coefficient d'absorption moyen de la salle. On en déduit le temps de réverbération de la salle Tr.
Connaissant le facteur de directivité des enceintes Q, on peut également calculer la distance critique dc, distance à laquelle l'intensité du champ sonore direct est égale à celle du champ réverbéré.
En combinant les équations exprimant la valeur du Tr et de dc, on calcule la valeur de la distance critique en fonction de Q, de V et de Tr. Cette valeur est proportionnelle à la racine carrée du rapport du volume sur le temps de réverbération.
L'expression de la valeur de la fréquence de Schroeder Fs (sur laquelle nous reviendrons en détail) est, quant à elle, proportionnelle à la racine carrée du temps de réverbération sur le volume.
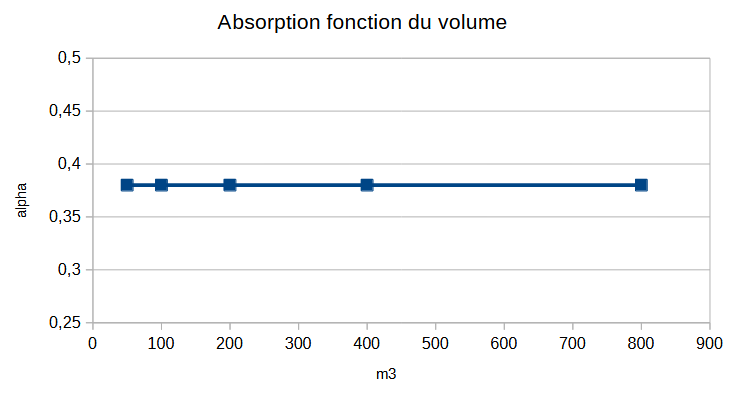
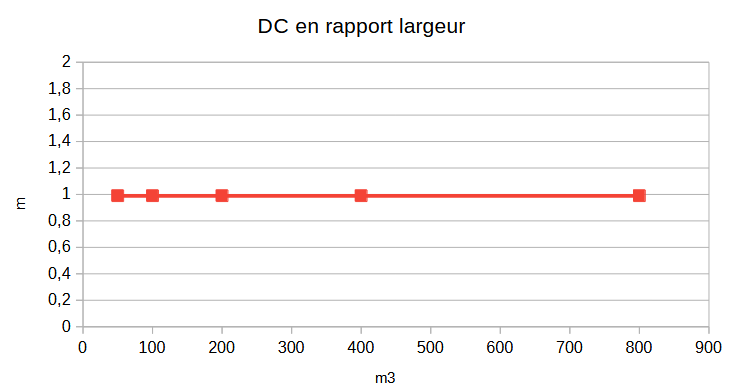
En combinant ces deux équations, on arrive à la conclusion que le produit de la distance critique par la fréquence de Schroeder ne dépend plus de la salle, mais uniquement du facteur de directivité des enceintes.
On peut en déduire une première conclusion : augmenter la taille d'une pièce sans augmenter la distance critique conduit à ne pas changer la fréquence de Schroeder.
Nous allons comparer trois salles de différents volumes. Pour bien quantifier l'influence de seulement le volume, nous prendrons les mêmes ratios concernant les proportions de ces salles. Le ratio choisi est : rapport longueur/hauteur : 2.1 ; rapport largeur/hauteur 1.45. Ce ratio a été optimisé selon le critère de Louden. Nous choisirons comme hauteur : 2.8 m, 4 m et 6.5 m. Les rapports de hauteur de ces salles sont : 1.43 et 2.32
À partir de ces ratios, on déduit facilement les variations de volume et de surface de ces pièces.
Pour examiner comment varient les paramètres acoustiques (Tr,dc,Fs), il nous faut faire une autre hypothèse. Nous avons vu qu'il est nécessaire d'augmenter la valeur de la distance critique quand on augmente le volume d'une pièce pour abaisser la fréquence de Schroeder. Nous choisirons donc de faire varier la distance critique de la même manière que varie la hauteur de ces différentes salles.
Cette hypothèse est logique puisque toutes les dimensions de ces salles varient du même facteur. Si on double la largeur, on peut s'attendre à doubler la distance du point d'écoute, et donc à doubler la valeur de la distance critique.
Nous choisirons enfin une distance du point d'écoute égale à 80% de la largeur de la salle.
Le calcul du temps de réverbération, formules d'Eyring :
Comme les salles que nous allons étudier sont fortement absorbées, il nous faut utiliser, pour calculer les coefficients d'absorption, la formule d'Eyring, la formule de Sabine n'étant plus valable lorsque ce coefficient est supérieur à 0.2.
Je donne les formules correspondantes qui ne sont pas plus compliquées. L'expression de la distance critique est identique en prenant, à la place de l'aire d'absorption acoustique A, la constante de la salle notée R.
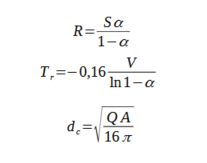 Il nous reste à effectuer un dernier calcul qui est la puissance de l'amplificateur qui alimente les enceintes. On suppose pour cela une efficacité des enceintes de 105 dB, un SPL max souhaité au PE de 105 dB avec une marge de 10 dB. On peut discuter de ces valeurs, mais l'important est de mesurer les écarts de puissances entre les salles.
Il nous reste à effectuer un dernier calcul qui est la puissance de l'amplificateur qui alimente les enceintes. On suppose pour cela une efficacité des enceintes de 105 dB, un SPL max souhaité au PE de 105 dB avec une marge de 10 dB. On peut discuter de ces valeurs, mais l'important est de mesurer les écarts de puissances entre les salles.
Pour réaliser tous ces calculs, j'ai réalisé un tableur Excel dont le lien est donné à la fin de ce message.
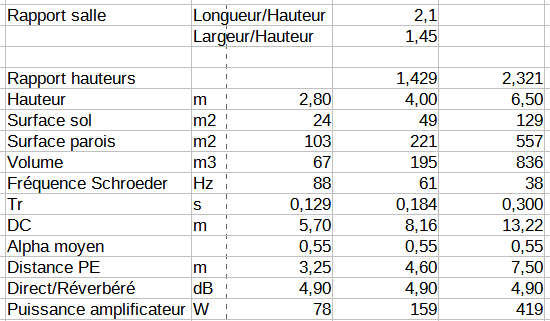
À partir de ces hypothèses et des formules ci-dessus codées dans le tableur, on obtient les caractéristiques suivantes concernant ces trois salles :
On peut faire les remarques suivantes :
Le temps de réverbération des modes :
Les calculs précédents (Tr, Fs) résultent d'une analyse statistique en considérant le champ diffus. Il est évident que dans le domaine des basses fréquences (inférieures à 100 hz) le champ n'est plus diffus, d'autant plus que les temps de réverbération sont faibles.
Il est donc intéressant de calculer le temps de réverbération de chaque mode et non pas un temps de réverbération unique. Pour comprendre la démarche, revenons sur la formule du temps de réverbération d'Eyring en décrivant comment on l'obtient.
On suppose que la densité d'énergie stationnaire dans une pièce est E0. À l'instant t=0, on coupe la source. À la première réflexion, la paroi va absorber l'énergie α E0. L'énergie restante est alors E1 = E0 (1- α). Au bout de N réflexions, l'énergie sera EN = E0 (1- α)^N. On peut alors calculer N pour que la baisse de niveau d'énergie entre E0 et EN soit de -60 dB.
Il reste à présent à lier N à la durée. Pour cela, on calcule ce qu'on appelle le libre parcours moyen exprimé en mètres. Si l'on considère dans un premier temps uniquement les ondes axiales se déplaçant dans le sens de la longueur de la salle, la distance entre deux réflexions va simplement être la longueur de la salle. Il va en être de même pour les autres ondes axiales concernant la hauteur et la largeur. On peut ainsi calculer le libre parcours moyen des ondes axiales en calculant la moyenne de la hauteur, de la largeur et de la longueur.
Mais, il nous faut aussi prendre en compte toutes les directions des ondes. Ce calcul amène au résultat suivant : le libre parcours moyen dans une salle s'exprime par lm = 4V/S. Il ne dépend que du volume et de la surface des parois de la pièce. En divisant cette valeur par la vitesse du son, on déduit le temps moyen que mettent les ondes sonores pour se réfléchir et on obtient l'expression du temps de réverbération d'Eyring.
On comprend ainsi la raison pour laquelle une grande salle à nécessairement un temps de réverbération élevé : le libre parcours moyen est plus important puisque le rapport V/S croît avec le volume.
Ainsi, étant donné que nous avons le même coefficient d'absorption moyen dans nos trois salles, les nombres de réflexions (N) pendant le temps de réverbération sont identiques. Le temps de réverbération de la grande salle augmente seulement parce que le libre parcours moyen augmente.
Cette valeur statistique de 4V/S est éloignée de ce qui se passe dans les modes en basses fréquences. Il est préférable de calculer le libre parcours moyen pour chaque mode et d'en déduire le temps de réverbération de chaque mode.
On trouvera à ce lien un article qui détaille ce calcul : Modal Reverberation Time
Je mets ici les formules codées dans le tableur Excel :
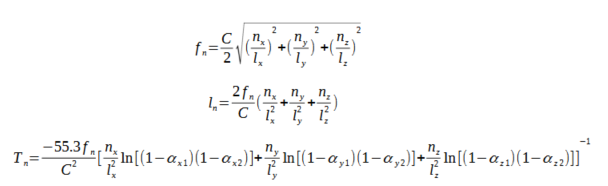 La démarche est la suivante : on considère des coefficients d'absorption constants par paroi : αx1 et αx2 pour le mur de devant et du fond, αy1 et αy2 les murs latéraux et αz1 et αz2 le plafond et le sol, nx, ny, nz sont les entiers qui définissent les modes. ln est le parcours moyen du mode et Tn le temps de réverbération du mode.
La démarche est la suivante : on considère des coefficients d'absorption constants par paroi : αx1 et αx2 pour le mur de devant et du fond, αy1 et αy2 les murs latéraux et αz1 et αz2 le plafond et le sol, nx, ny, nz sont les entiers qui définissent les modes. ln est le parcours moyen du mode et Tn le temps de réverbération du mode.
On peut alors tracer les temps de réverbération de chaque mode pour les trois salles considérées. Notons que lorsque deux des coefficients parmi nx,ny,nz sont nuls, les formules se simplifient et le temps de réverbération devient constant quel que soit le mode. Ces tracés ont été réalisés avec un Script Scilab (voir la fin de ce message).
Voici les valeurs pour les fréquences de 0 à 100 hz et de 200 à 400 hz. Les valeurs les plus élevées correspondent aux modes longitudinaux :
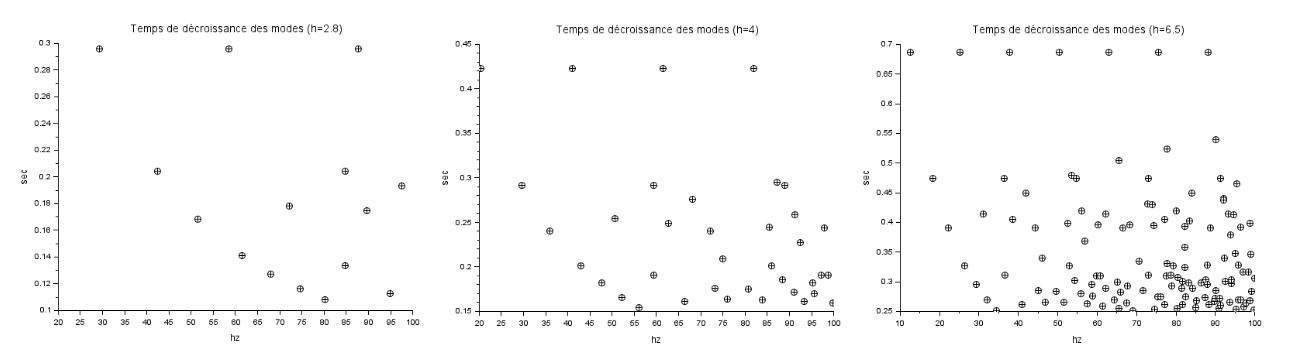
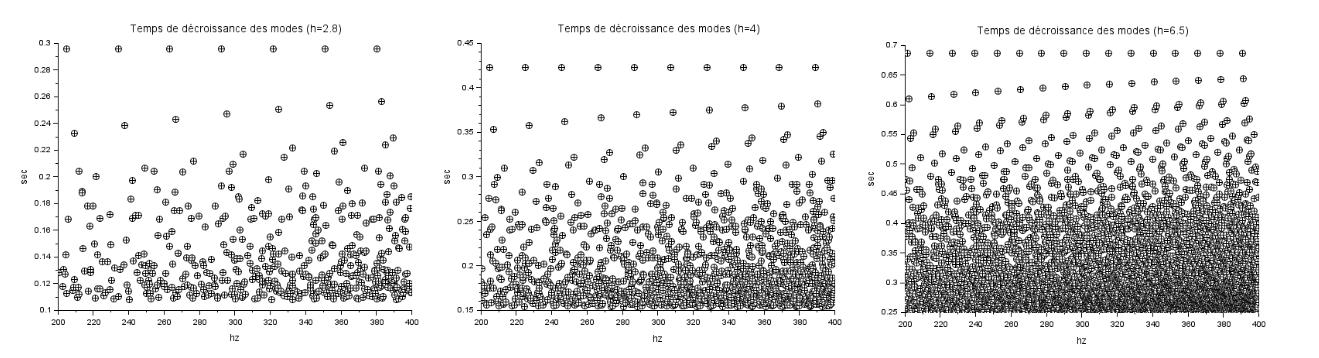
Il devient alors intéressant de calculer la moyenne du libre parcours moyen des modes par 1/3 d'octave et de calculer le temps de réverbération correspondant. Voici ce qu'on obtient :
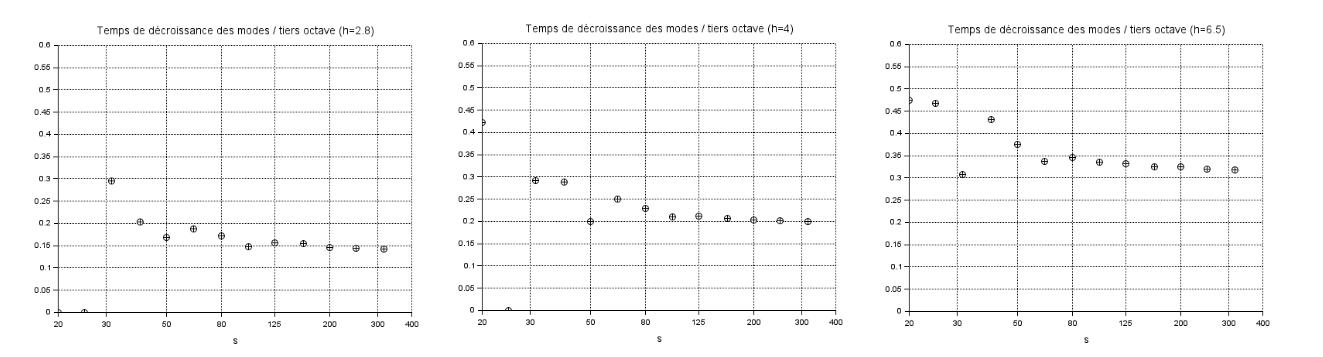 Ces courbes donnent le véritable temps de réverbération des modes. On remarque que le temps de décroissance des modes augmente plus la fréquence baisse. La valeur tend vers le temps de réverbération de la salle en haute fréquences.
Ces courbes donnent le véritable temps de réverbération des modes. On remarque que le temps de décroissance des modes augmente plus la fréquence baisse. La valeur tend vers le temps de réverbération de la salle en haute fréquences.
On comprend mieux pourquoi il est difficile d'amortir les modes en basses fréquences. Non seulement le traitement acoustique pour atteindre un faible coefficient d'absorption est difficile à réaliser vu les importantes longueurs d'onde, mais du fait d'un libre parcours qui augmente, pour une même valeur du coefficient, le temps de décroissance en basse fréquence augmente.
Il est intéressant de faire remarquer que c'est dans la plus grande salle que le temps de décroissance des modes augmente le moins en rapport du temps de réverbération.
La fréquence de Scroeder :
Il faut savoir que la fréquence de Schroeder ne définit pas une frontière nette entre le champ diffus et la zone modale.
Pour comprendre comment intervient le temps de réverbération dans la fréquence de Schroeder, on peut exposer les bases de son calcul.
La base de ce calcul est l'espacement en fréquence entre les maximas des modes et la différence de niveau entre les maximas et minimas, comme le montre la figure suivante :
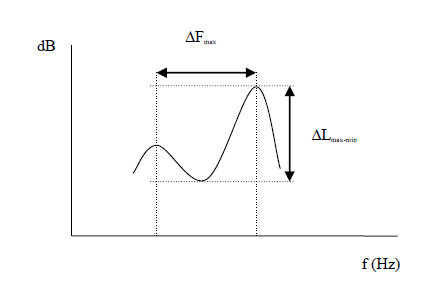
Deux équations permettent d'arriver à l'expression de la fréquence de Schroeder qui sont :
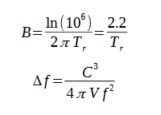 La première formule donne la largeur de bande B à mi-puissance des modes. Cette largeur de bande est simplement inversement proportionnelle au temps de réverbération. C'est somme toute logique : dans une pièce réverbérante (tr élevé), les modes sont des pics abrupts. Plus on amortit la salle (tr faible), plus le pic diminue et plus le mode s'étale.
La première formule donne la largeur de bande B à mi-puissance des modes. Cette largeur de bande est simplement inversement proportionnelle au temps de réverbération. C'est somme toute logique : dans une pièce réverbérante (tr élevé), les modes sont des pics abrupts. Plus on amortit la salle (tr faible), plus le pic diminue et plus le mode s'étale.
La seconde formule donne Δf l'écartement en fréquence des modes pour une fréquence donnée. Plus la fréquence augmente, plus l'écart entre les modes baisse. Plus le volume de la salle augmente, plus l'écart entre les modes baisse.
La fréquence de Schroeder consiste à fixer le rapport entre B et Δf en posant B = 3 Δf. Des deux formules ci-dessus, on déduit alors l'expression de renom de la fréquence de Schroeder.
Notons qu'initialement Schroeder avait suggéré d'utiliser B = 10 Δf ce qui donnait une fréquence double de la valeur actuelle.
On comprend bien la raison pour laquelle le temps de réverbération intervient dans cette formule. Il ne suffit pas qu'il y ait beaucoup de mode, il faut également que l'écart entre les modes soit plus faible que la largeur de bande des modes pour lisser la réponse en fréquence.
Ainsi, pour une fréquence de Schroeder faible, il est préférable d'avoir une salle de grand volume (Δf faible) mais aussi une bande B importante, ce qui conduit à un tr faible.
Ces deux conditions sont peu compatibles parce que le libre parcours moyen (comme nous l'avons vu) d'une grande salle est nécessairement élevé, ce qui conduit naturellement à un Tr plus élevé.
La zone de transition entre le régime modal et le champ diffus n'est en réalité pas une fréquence parfaitement déterminée, mais une zone dont la fréquence de Schroeder définit plutôt la limite haute. On trouvera à ce lien un article qui donnera plus d'informations : Schroeder Frequency Revisited
Pour mieux quantifier ce qui se passe en basse fréquence, il est préférable, pour une salle donnée, de calculer les modes et de calculer les écarts entre ces modes plutôt que d'utiliser la formule ci-dessus qui n'est vraiment valide que dans le champ diffus.
On peut alors calculer la fréquence à partir de laquelle les écarts de fréquences entre deux modes successifs sont toujours inférieurs à la bande à demi-puissance divisée par trois pour reprendre la condition de Schroeder.
Ce résultat est exprimé dans le tableau suivant :
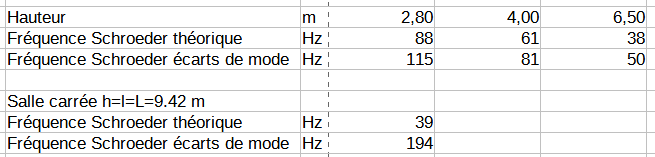
On trouve respectivement de la petite salle à la plus grande : 115 hz, 81 hz et 50 hz. On remarque que ces valeurs sont plus élevées que celles obtenues avec la formule classique de la fréquence de Schroëder. Le critère est plus sévère car il ne porte pas sur une moyenne.
L'intérêt de ce critère est de tenir compte des modes réels de la salle. Pour s'en convaincre, on a calculé la valeur de cette fréquence pour une salle cubique de même volume que la grande salle. On trouve 194 hz au lieu de 50 hz. Une grande salle ne permet pas de s'affranchir de rapports adéquats.
La valeur absolue du temps de réverbération :
Nous avons vu que le temps de réverbération dans une grande salle est nécessairement plus important que dans une plus petite du fait d'un libre parcours moyen plus élevé. La grande salle a un temps de réverbération de 0.3 s.
Lorsqu'on reproduit de la musique avec des enceintes, il y a superposition de deux champs réverbérés : celui de la salle d'enregistrement (que l'on nommera studio) et celui de la salle d'écoute (que l'on nommera auditorium).
On peut calculer le niveau sonore dans l'auditorium à partir du champ direct et réverbéré de cette salle et de la différence de niveau initial entre ces deux champs.
Lorsque le signal sonore s'arrête dans le studio, les enceintes transmettent le champ réverbéré du studio (courbe en bleu des prochains diagrammes). C'est ce son que devrait entendre un auditeur dans l'auditorium. Il se superpose à ce signal (courbe bleue) le champ réverbéré de l'auditorium (courbe verte). L'intensité totale est la somme des deux intensités (courbe rouge).
Dans le premier cas, on place l'auditeur au-delà de la distance critique de telle manière que le niveau du champ direct soit 3 db au-dessous du champ réverbéré. On prend un tr studio de 0.2 s et un tr de l'auditorium de 0.3 s.
Voici ce qu'on obtient :
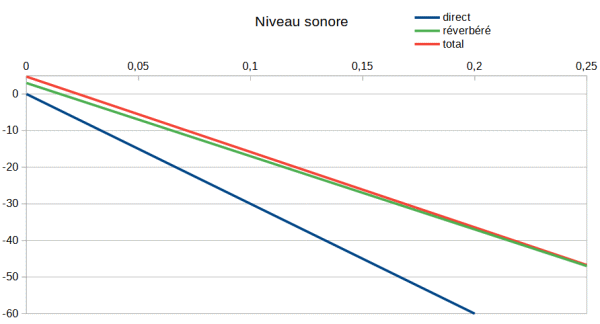 Alors que l'auditeur devrait percevoir la courbe bleue, il perçoit la courbe rouge confondue avec la courbe verte. L'acoustique de l'auditorium masque l'acoustique du studio.
Alors que l'auditeur devrait percevoir la courbe bleue, il perçoit la courbe rouge confondue avec la courbe verte. L'acoustique de l'auditorium masque l'acoustique du studio.
Plaçons-nous maintenant dans le cas où les temps de réverbération sont inchangés, mais l'auditeur placé en deçà de la distance critique avec un niveau du champ direct 3 dB au-dessus du champ réverbéré. On obtient :
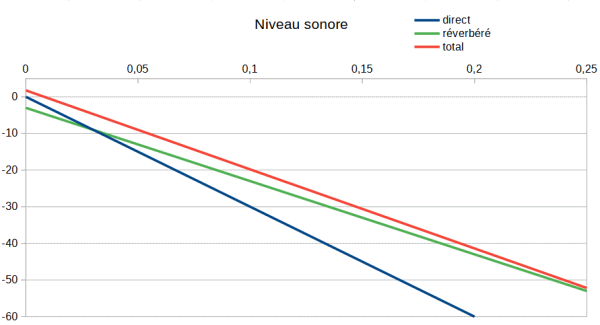
Le signal perçu par l'auditeur s'approche du signal entendu dans le studio un court instant. Mais, le temps de réverbération plus élevé dans l'auditorium que dans le studio finit par masquer le signal émis dans le studio.
Prenons à présent un dernier cas, où le temps de réverbération de l'auditorium est de 0.2 s. Cette fois, le signal entendu est très proche du signal retransmis.
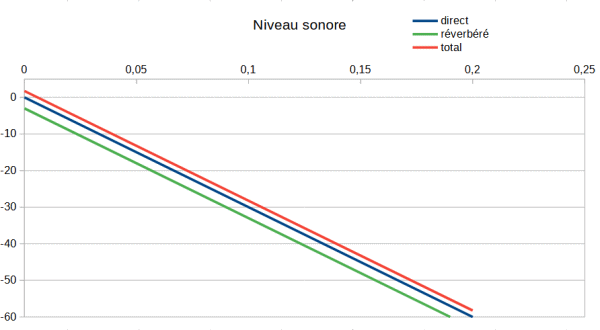
Pour que l'acoustique de l'auditorium ne masque pas l'acoustique du studio, il est nécessaire de remplir deux conditions : l'intensité du champ direct doit être supérieure à l'intensité du champ réverbéré et le temps de réverbération de l'auditorium doit être inférieur ou égal au temps de réverbération du studio.
Cet argument ne milite pas en faveur de très grandes salles.
Simulation du niveau SPL
Un autre critère à prendre en compte est évidemment la réponse de l'enceinte dans la pièce. Celle-ci peut se calculer à partir de l'équation de résolution des modes en calculant le temps de décroissance de chaque mode. Ce calcul peut être fait par REW dans la partie "Room simulation". J'ai réalisé un Script Scilab qui fait ce calcul.
Voici ce que donne la réponse en l'absence d'absorbant en plaçant l'enceinte dans un coin et le microphone de mesure au coin opposé pour être sûr d'exciter un maximum de mode :
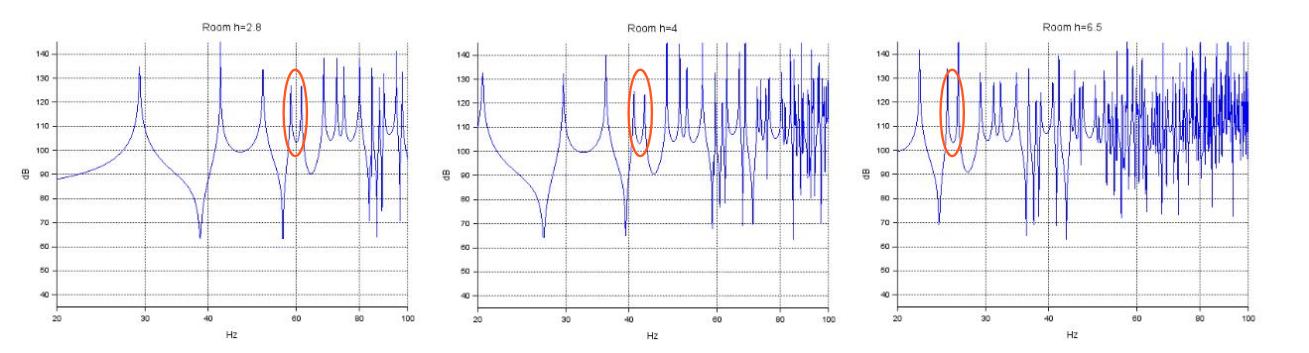 On remarque bien la densité des modes qui augmente avec la taille de la pièce. En réalité, ces réponses sont homothétiques, car les trois pièces ont les mêmes ratios de dimension. La réponse autour de 60 hz dans la petite salle correspond à la réponse autour de 45 hz dans la salle intermédiaire et 25 hz dans la grande salle.
On remarque bien la densité des modes qui augmente avec la taille de la pièce. En réalité, ces réponses sont homothétiques, car les trois pièces ont les mêmes ratios de dimension. La réponse autour de 60 hz dans la petite salle correspond à la réponse autour de 45 hz dans la salle intermédiaire et 25 hz dans la grande salle.
Avec un coefficient d'absorption de 0.55 on obtient les courbes suivantes :
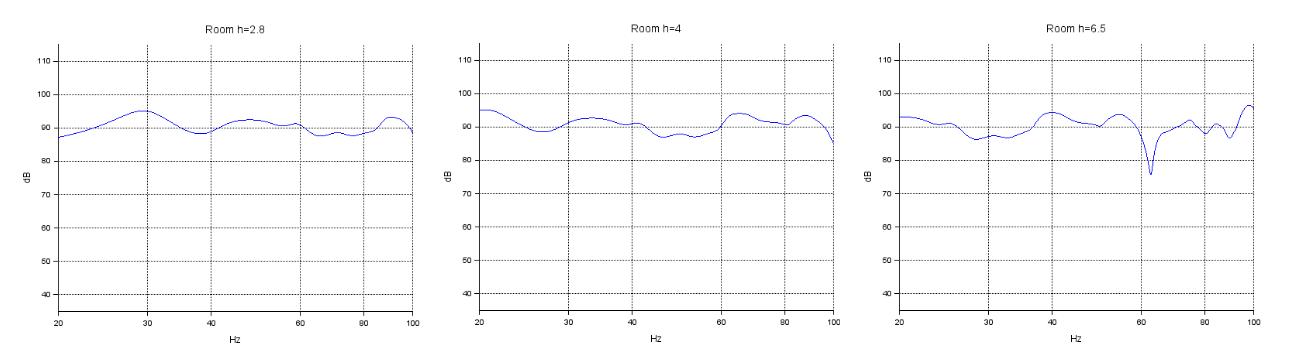
La réponse est lissée par l'important coefficient d'absorption. La grande pièce n'offre pas réellement plus d'avantages.
Conclusion
Le choix de la taille d'une salle dépend de plusieurs critères et résulte nécessairement de compromis.
Si l'on se place du point de vue purement acoustique, on peut dire :
Dans les exemples simulés, le coefficient d'absorption est de 0.55. C'est un coefficient qui ne peut être obtenu en très basses fréquences qu'avec un traitement important et de forte épaisseur.
Si l'on considère que ce traitement conduit à une épaisseur d'environ 1 m, on constatera que la salle de 2.8 m de hauteur ne fait plus que 1.8 m x 2.06-m x 4.88 m (je n'ai pas traité le sol et le mur des enceintes). Elle se réduit à peau de chagrin. Celle de 4 m fera 3 m x 3.8 m x 7.4 m.
Dans les exemples choisis, la salle de hauteur 4 m, me parait être le meilleur compromis. Ca reste une grande salle dont le volume brut est de 195 m3 avec une hauteur, rappelons le de 4 m.
Evidemment pour limiter l'épaisseur du traitement acoustique, on peut optimiser les placement des sub (SBA, DBA ou autre). Mais c'est une autre histoire ...
Cordialement
Jean
PS :
lien vers le tableur Excel :Room simulation
lien vers le script Scilab de calcul de l'amortissement des modes : :TR modes
lien vers le script Scilab de calcul de la réponse SPL des modes : :Room simulation
On sait tous qu'un des problèmes majeurs en acoustique concerne le traitement des modes en basses fréquences. Ces modes dépendent fortement de la géométrie de la pièce et de ses dimensions.
L'idéal serait d'être dénué de tout régime modal. On connait la fréquence de Schröder qui fixe la limite entre le régime diffus et le régime modal. Cette fréquence peut-elle être suffisamment basse pour éviter un traitement acoustique lourd dans les basses fréquences ?
L'objet de ce post est d'aborder le problème des modes en basses fréquences et de quantifier l'importance de la taille de la salle.
Le calcul du temps de réverbération, formules de Sabine :
Rappelons quelques formules concernant le calcul du temps de réverbération selon la formulation de Sabine. Nous avons :
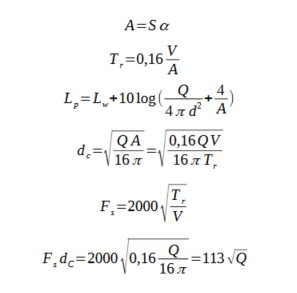
Connaissant le facteur de directivité des enceintes Q, on peut également calculer la distance critique dc, distance à laquelle l'intensité du champ sonore direct est égale à celle du champ réverbéré.
En combinant les équations exprimant la valeur du Tr et de dc, on calcule la valeur de la distance critique en fonction de Q, de V et de Tr. Cette valeur est proportionnelle à la racine carrée du rapport du volume sur le temps de réverbération.
L'expression de la valeur de la fréquence de Schroeder Fs (sur laquelle nous reviendrons en détail) est, quant à elle, proportionnelle à la racine carrée du temps de réverbération sur le volume.
En combinant ces deux équations, on arrive à la conclusion que le produit de la distance critique par la fréquence de Schroeder ne dépend plus de la salle, mais uniquement du facteur de directivité des enceintes.
On peut en déduire une première conclusion : augmenter la taille d'une pièce sans augmenter la distance critique conduit à ne pas changer la fréquence de Schroeder.
Nous allons comparer trois salles de différents volumes. Pour bien quantifier l'influence de seulement le volume, nous prendrons les mêmes ratios concernant les proportions de ces salles. Le ratio choisi est : rapport longueur/hauteur : 2.1 ; rapport largeur/hauteur 1.45. Ce ratio a été optimisé selon le critère de Louden. Nous choisirons comme hauteur : 2.8 m, 4 m et 6.5 m. Les rapports de hauteur de ces salles sont : 1.43 et 2.32
À partir de ces ratios, on déduit facilement les variations de volume et de surface de ces pièces.
Pour examiner comment varient les paramètres acoustiques (Tr,dc,Fs), il nous faut faire une autre hypothèse. Nous avons vu qu'il est nécessaire d'augmenter la valeur de la distance critique quand on augmente le volume d'une pièce pour abaisser la fréquence de Schroeder. Nous choisirons donc de faire varier la distance critique de la même manière que varie la hauteur de ces différentes salles.
Cette hypothèse est logique puisque toutes les dimensions de ces salles varient du même facteur. Si on double la largeur, on peut s'attendre à doubler la distance du point d'écoute, et donc à doubler la valeur de la distance critique.
Nous choisirons enfin une distance du point d'écoute égale à 80% de la largeur de la salle.
Le calcul du temps de réverbération, formules d'Eyring :
Comme les salles que nous allons étudier sont fortement absorbées, il nous faut utiliser, pour calculer les coefficients d'absorption, la formule d'Eyring, la formule de Sabine n'étant plus valable lorsque ce coefficient est supérieur à 0.2.
Je donne les formules correspondantes qui ne sont pas plus compliquées. L'expression de la distance critique est identique en prenant, à la place de l'aire d'absorption acoustique A, la constante de la salle notée R.
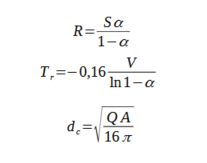
Pour réaliser tous ces calculs, j'ai réalisé un tableur Excel dont le lien est donné à la fin de ce message.
À partir de ces hypothèses et des formules ci-dessus codées dans le tableur, on obtient les caractéristiques suivantes concernant ces trois salles :

On peut faire les remarques suivantes :
- Le volume varie de 67 m3 à 836 m3, et le temps de réverbération de 0.129 s à 0.3 s.
- La puissance passe de 78 W à 419 W. La puissance en elle-même n'est pas un problème, les amplificateurs modernes permettront de l'atteindre facilement. Reste quand même le problème de la distorsion des enceintes. Ce point est en défaveur des grandes salles.
- Le temps de réverbération augmente avec la taille de la pièce en rapport des hauteurs. On passe de 0.120 s à 0.3 s. Nous reviendrons en détail sur ce point.
- Le coefficient d'absorption moyen est identique. Autrement dit, le traitement acoustique doit être équivalent. Ceci répond déjà à une question : les grandes salles ne permettent pas de diminuer l'épaisseur du traitement acoustique (nous préciserons ce point en ce qui concerne les basses fréquences un peu plus loin).
- La fréquence de Schroeder est respectivement de 88 hz, 61 hz et 38 hz de la plus petite salle à la plus grande. Le rapport des fréquences de Schroeder est égal au rapport des hauteurs. Autrement dit, avec les hypothèses considérées, la fréquence de Schroeder varie proportionnellement à l'inverse de la racine cubique du volume.
Le temps de réverbération des modes :
Les calculs précédents (Tr, Fs) résultent d'une analyse statistique en considérant le champ diffus. Il est évident que dans le domaine des basses fréquences (inférieures à 100 hz) le champ n'est plus diffus, d'autant plus que les temps de réverbération sont faibles.
Il est donc intéressant de calculer le temps de réverbération de chaque mode et non pas un temps de réverbération unique. Pour comprendre la démarche, revenons sur la formule du temps de réverbération d'Eyring en décrivant comment on l'obtient.
On suppose que la densité d'énergie stationnaire dans une pièce est E0. À l'instant t=0, on coupe la source. À la première réflexion, la paroi va absorber l'énergie α E0. L'énergie restante est alors E1 = E0 (1- α). Au bout de N réflexions, l'énergie sera EN = E0 (1- α)^N. On peut alors calculer N pour que la baisse de niveau d'énergie entre E0 et EN soit de -60 dB.
Il reste à présent à lier N à la durée. Pour cela, on calcule ce qu'on appelle le libre parcours moyen exprimé en mètres. Si l'on considère dans un premier temps uniquement les ondes axiales se déplaçant dans le sens de la longueur de la salle, la distance entre deux réflexions va simplement être la longueur de la salle. Il va en être de même pour les autres ondes axiales concernant la hauteur et la largeur. On peut ainsi calculer le libre parcours moyen des ondes axiales en calculant la moyenne de la hauteur, de la largeur et de la longueur.
Mais, il nous faut aussi prendre en compte toutes les directions des ondes. Ce calcul amène au résultat suivant : le libre parcours moyen dans une salle s'exprime par lm = 4V/S. Il ne dépend que du volume et de la surface des parois de la pièce. En divisant cette valeur par la vitesse du son, on déduit le temps moyen que mettent les ondes sonores pour se réfléchir et on obtient l'expression du temps de réverbération d'Eyring.
On comprend ainsi la raison pour laquelle une grande salle à nécessairement un temps de réverbération élevé : le libre parcours moyen est plus important puisque le rapport V/S croît avec le volume.
Ainsi, étant donné que nous avons le même coefficient d'absorption moyen dans nos trois salles, les nombres de réflexions (N) pendant le temps de réverbération sont identiques. Le temps de réverbération de la grande salle augmente seulement parce que le libre parcours moyen augmente.
Cette valeur statistique de 4V/S est éloignée de ce qui se passe dans les modes en basses fréquences. Il est préférable de calculer le libre parcours moyen pour chaque mode et d'en déduire le temps de réverbération de chaque mode.
On trouvera à ce lien un article qui détaille ce calcul : Modal Reverberation Time
Je mets ici les formules codées dans le tableur Excel :
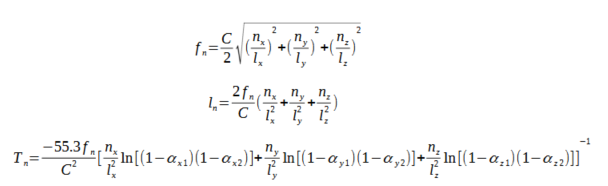
On peut alors tracer les temps de réverbération de chaque mode pour les trois salles considérées. Notons que lorsque deux des coefficients parmi nx,ny,nz sont nuls, les formules se simplifient et le temps de réverbération devient constant quel que soit le mode. Ces tracés ont été réalisés avec un Script Scilab (voir la fin de ce message).
Voici les valeurs pour les fréquences de 0 à 100 hz et de 200 à 400 hz. Les valeurs les plus élevées correspondent aux modes longitudinaux :


Il devient alors intéressant de calculer la moyenne du libre parcours moyen des modes par 1/3 d'octave et de calculer le temps de réverbération correspondant. Voici ce qu'on obtient :

On comprend mieux pourquoi il est difficile d'amortir les modes en basses fréquences. Non seulement le traitement acoustique pour atteindre un faible coefficient d'absorption est difficile à réaliser vu les importantes longueurs d'onde, mais du fait d'un libre parcours qui augmente, pour une même valeur du coefficient, le temps de décroissance en basse fréquence augmente.
Il est intéressant de faire remarquer que c'est dans la plus grande salle que le temps de décroissance des modes augmente le moins en rapport du temps de réverbération.
La fréquence de Scroeder :
Il faut savoir que la fréquence de Schroeder ne définit pas une frontière nette entre le champ diffus et la zone modale.
Pour comprendre comment intervient le temps de réverbération dans la fréquence de Schroeder, on peut exposer les bases de son calcul.
La base de ce calcul est l'espacement en fréquence entre les maximas des modes et la différence de niveau entre les maximas et minimas, comme le montre la figure suivante :

Deux équations permettent d'arriver à l'expression de la fréquence de Schroeder qui sont :
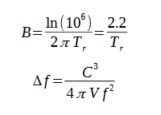
La seconde formule donne Δf l'écartement en fréquence des modes pour une fréquence donnée. Plus la fréquence augmente, plus l'écart entre les modes baisse. Plus le volume de la salle augmente, plus l'écart entre les modes baisse.
La fréquence de Schroeder consiste à fixer le rapport entre B et Δf en posant B = 3 Δf. Des deux formules ci-dessus, on déduit alors l'expression de renom de la fréquence de Schroeder.
Notons qu'initialement Schroeder avait suggéré d'utiliser B = 10 Δf ce qui donnait une fréquence double de la valeur actuelle.
On comprend bien la raison pour laquelle le temps de réverbération intervient dans cette formule. Il ne suffit pas qu'il y ait beaucoup de mode, il faut également que l'écart entre les modes soit plus faible que la largeur de bande des modes pour lisser la réponse en fréquence.
Ainsi, pour une fréquence de Schroeder faible, il est préférable d'avoir une salle de grand volume (Δf faible) mais aussi une bande B importante, ce qui conduit à un tr faible.
Ces deux conditions sont peu compatibles parce que le libre parcours moyen (comme nous l'avons vu) d'une grande salle est nécessairement élevé, ce qui conduit naturellement à un Tr plus élevé.
La zone de transition entre le régime modal et le champ diffus n'est en réalité pas une fréquence parfaitement déterminée, mais une zone dont la fréquence de Schroeder définit plutôt la limite haute. On trouvera à ce lien un article qui donnera plus d'informations : Schroeder Frequency Revisited
Pour mieux quantifier ce qui se passe en basse fréquence, il est préférable, pour une salle donnée, de calculer les modes et de calculer les écarts entre ces modes plutôt que d'utiliser la formule ci-dessus qui n'est vraiment valide que dans le champ diffus.
On peut alors calculer la fréquence à partir de laquelle les écarts de fréquences entre deux modes successifs sont toujours inférieurs à la bande à demi-puissance divisée par trois pour reprendre la condition de Schroeder.
Ce résultat est exprimé dans le tableau suivant :

On trouve respectivement de la petite salle à la plus grande : 115 hz, 81 hz et 50 hz. On remarque que ces valeurs sont plus élevées que celles obtenues avec la formule classique de la fréquence de Schroëder. Le critère est plus sévère car il ne porte pas sur une moyenne.
L'intérêt de ce critère est de tenir compte des modes réels de la salle. Pour s'en convaincre, on a calculé la valeur de cette fréquence pour une salle cubique de même volume que la grande salle. On trouve 194 hz au lieu de 50 hz. Une grande salle ne permet pas de s'affranchir de rapports adéquats.
La valeur absolue du temps de réverbération :
Nous avons vu que le temps de réverbération dans une grande salle est nécessairement plus important que dans une plus petite du fait d'un libre parcours moyen plus élevé. La grande salle a un temps de réverbération de 0.3 s.
Lorsqu'on reproduit de la musique avec des enceintes, il y a superposition de deux champs réverbérés : celui de la salle d'enregistrement (que l'on nommera studio) et celui de la salle d'écoute (que l'on nommera auditorium).
On peut calculer le niveau sonore dans l'auditorium à partir du champ direct et réverbéré de cette salle et de la différence de niveau initial entre ces deux champs.
Lorsque le signal sonore s'arrête dans le studio, les enceintes transmettent le champ réverbéré du studio (courbe en bleu des prochains diagrammes). C'est ce son que devrait entendre un auditeur dans l'auditorium. Il se superpose à ce signal (courbe bleue) le champ réverbéré de l'auditorium (courbe verte). L'intensité totale est la somme des deux intensités (courbe rouge).
Dans le premier cas, on place l'auditeur au-delà de la distance critique de telle manière que le niveau du champ direct soit 3 db au-dessous du champ réverbéré. On prend un tr studio de 0.2 s et un tr de l'auditorium de 0.3 s.
Voici ce qu'on obtient :

Plaçons-nous maintenant dans le cas où les temps de réverbération sont inchangés, mais l'auditeur placé en deçà de la distance critique avec un niveau du champ direct 3 dB au-dessus du champ réverbéré. On obtient :

Le signal perçu par l'auditeur s'approche du signal entendu dans le studio un court instant. Mais, le temps de réverbération plus élevé dans l'auditorium que dans le studio finit par masquer le signal émis dans le studio.
Prenons à présent un dernier cas, où le temps de réverbération de l'auditorium est de 0.2 s. Cette fois, le signal entendu est très proche du signal retransmis.

Pour que l'acoustique de l'auditorium ne masque pas l'acoustique du studio, il est nécessaire de remplir deux conditions : l'intensité du champ direct doit être supérieure à l'intensité du champ réverbéré et le temps de réverbération de l'auditorium doit être inférieur ou égal au temps de réverbération du studio.
Cet argument ne milite pas en faveur de très grandes salles.
Simulation du niveau SPL
Un autre critère à prendre en compte est évidemment la réponse de l'enceinte dans la pièce. Celle-ci peut se calculer à partir de l'équation de résolution des modes en calculant le temps de décroissance de chaque mode. Ce calcul peut être fait par REW dans la partie "Room simulation". J'ai réalisé un Script Scilab qui fait ce calcul.
Voici ce que donne la réponse en l'absence d'absorbant en plaçant l'enceinte dans un coin et le microphone de mesure au coin opposé pour être sûr d'exciter un maximum de mode :

Avec un coefficient d'absorption de 0.55 on obtient les courbes suivantes :

La réponse est lissée par l'important coefficient d'absorption. La grande pièce n'offre pas réellement plus d'avantages.
Conclusion
Le choix de la taille d'une salle dépend de plusieurs critères et résulte nécessairement de compromis.
Si l'on se place du point de vue purement acoustique, on peut dire :
- Les très grandes salles ont le bénéfice d'une densité modale plus importante et permettent de baisser la fréquence de Schroeder. Cela conduit en théorie à mieux lisser la réponse dans les très basses fréquences. Cependant, la fréquence de Schroeder ne baisse que si l'absorption reste importante.
- Les réponses en fréquences de plus petites salles ne sont pas obligatoirement plus perturbées si les coefficients d'absorption restent importants, très bas en fréquence.
- Un inconvénient des grandes salles est le temps de réverbération plus élevé et une distorsion au PE plus importante étant donné les puissances électriques nécessaires.
Dans les exemples simulés, le coefficient d'absorption est de 0.55. C'est un coefficient qui ne peut être obtenu en très basses fréquences qu'avec un traitement important et de forte épaisseur.
Si l'on considère que ce traitement conduit à une épaisseur d'environ 1 m, on constatera que la salle de 2.8 m de hauteur ne fait plus que 1.8 m x 2.06-m x 4.88 m (je n'ai pas traité le sol et le mur des enceintes). Elle se réduit à peau de chagrin. Celle de 4 m fera 3 m x 3.8 m x 7.4 m.
Dans les exemples choisis, la salle de hauteur 4 m, me parait être le meilleur compromis. Ca reste une grande salle dont le volume brut est de 195 m3 avec une hauteur, rappelons le de 4 m.
Evidemment pour limiter l'épaisseur du traitement acoustique, on peut optimiser les placement des sub (SBA, DBA ou autre). Mais c'est une autre histoire ...
Cordialement
Jean
PS :
lien vers le tableur Excel :Room simulation
lien vers le script Scilab de calcul de l'amortissement des modes : :TR modes
lien vers le script Scilab de calcul de la réponse SPL des modes : :Room simulation