Bonjour à tous.
Vous pouvez désormais, si l'envie vous en dit, soutenir SoundPixelLab - Vous retrouverez les informations sur ce lien en dessous
Soutenir SoundPixelLab
Merci à vous !
Vous pouvez désormais, si l'envie vous en dit, soutenir SoundPixelLab - Vous retrouverez les informations sur ce lien en dessous
Soutenir SoundPixelLab
Merci à vous !
Les sondes de calibration
-
Emmanuel Piat
- 34 dB
- Messages : 72
- Enregistré le : 11 janv. 2026, 11:26
Re: Les sondes de calibration
L'analyse du point (2) n'était pas correcte. Je l'ai donc réécrite et j'ai ajouté en bas du post le profil du bruit qui a été calculé ainsi :
- j'ai passé un filtre de Savitzky-Golay sur Smes(lambda) pour obtenir un spectre Smes_filtré(lambda) sans bruit.
- j'ai plotté la différence noise(lambda) = Smes(lambda)-Smes_filtré(lambda) pour chaque lambda.
Le bruit noise(lambda) a une moyenne quasi nulle qui vaut 0.000002.
On voit que le bruit obtenu n'a pas un écart-type constant sur lambda. Le bruit augmente sous 475 nm et il augmente aussi après 500 nm. Donc le gain G(lambda) de la correction appliquée à ce spectro est une fct concave.
- j'ai passé un filtre de Savitzky-Golay sur Smes(lambda) pour obtenir un spectre Smes_filtré(lambda) sans bruit.
- j'ai plotté la différence noise(lambda) = Smes(lambda)-Smes_filtré(lambda) pour chaque lambda.
Le bruit noise(lambda) a une moyenne quasi nulle qui vaut 0.000002.
On voit que le bruit obtenu n'a pas un écart-type constant sur lambda. Le bruit augmente sous 475 nm et il augmente aussi après 500 nm. Donc le gain G(lambda) de la correction appliquée à ce spectro est une fct concave.
-
Emmanuel Piat
- 34 dB
- Messages : 72
- Enregistré le : 11 janv. 2026, 11:26
Re: Les sondes de calibration
Passons aux math...
Rappel des notations :
pour simplifier je note "l" la longueur d'onde lambda.
Smes(l) : le spectre normalisé mesuré qu'il faut corriger
S_cor(l) : le spectre normalisé corrigé qu'on veut calculer (CCT de 2796 K)
BB_2796(l) : le spectre normalisé du corps noir à T = 2796 K
BB_2610(l) : le spectre normalisé du corps noir à T = 2610.8 K
E_2610(l) : l'erreur relative entre Smes(lambda) et BB_2610(lambda)
T(l) : l'erreur relative cible par rapport à BT_2610 (courbe bleue tracé avec des splines)
Contrainte : on veut que T(l) soit également l'erreur relative de S_cor par rapport à BT_2796.
Exprimons E_2610(l), non pas en % mais entre 0 et 1 :
E_2610(l) = (Smes(l) - BB_2610(l)) / BB_2610(l)
E_2610(l) = Smes(l) / BB_2610(l) - 1
=> Smes(l) = (E_2610(l) + 1) x BB_2610(l) (Eq. 1)
Soit S(l) le spectre intermédiaire dont l'erreur relative par rapport à BB_2610 est la cible T :
T(l) = S(l) / BB_2610(l) - 1
=> S(l) = (T(l) + 1) x BB_2610(l) (Eq. 2)
On divise (Eq. 2) par (Eq. 1) :
S(l) / Smes(l) = (T(l) + 1) / (E_2610(l) + 1)
S(l) = Smes(l) x (T(l) + 1) / (E_2610(l) + 1)
On pose Correction(l) = (T(l) + 1) / (E_2610(l) + 1) (Eq. 3)
=> S(l) = Smes(l) x Correction(l) (Eq. 4)
La CCT de S(l) n'est pas 2796 K. Elle est proche de 2610 K (proche va dépendre du choix de T).
On veut que S_cor ait aussi T comme erreur relative par rapport à BB_2796 (c'est la contrainte) :
T(l) = S_cor(l) / BB_2796(l) - 1
=> S_cor(l) = (T(l) + 1) x BB_2796(l) (Eq. 5)
On divise (Eq. 5) par (Eq. 1) :
S_cor(l) / Smes(T) = (T(l) + 1) x BB_2796(l) / ((E_2610(l) + 1) x BB_2610(l))
S_cor(l) = Smes(l) x (T(l) + 1) x BB_2796(l) / ((E_2610(l) + 1) x BB_2610(l))
S_cor(l) = Smes(l) x (T(l) + 1) / (E_2610(l) + 1) x BB_2796(l) / BB_2610(l)
Voici donc la formule de correction de Smes :
=> S_cor(l) = Smes(l) x Correction(l) x BB_2796(l) / BB_2610(l) (Eq. 6)
avec Correction(l) donnée par l'Eq. 3.
La CCT de S_cor(l) est proche de 2796 K (proche va dépendre du choix de T).
Nota : le facteur d'ajustement qui permet de passer de S(l) à S_cor(l) est BB_2796(l) / BB_2610(l) puisqu'on a grâce à l'Eq. 4 :
S_cor(l) = S(l) x BB_2796(l) / BB_2610(l)
Rappel des notations :
pour simplifier je note "l" la longueur d'onde lambda.
Smes(l) : le spectre normalisé mesuré qu'il faut corriger
S_cor(l) : le spectre normalisé corrigé qu'on veut calculer (CCT de 2796 K)
BB_2796(l) : le spectre normalisé du corps noir à T = 2796 K
BB_2610(l) : le spectre normalisé du corps noir à T = 2610.8 K
E_2610(l) : l'erreur relative entre Smes(lambda) et BB_2610(lambda)
T(l) : l'erreur relative cible par rapport à BT_2610 (courbe bleue tracé avec des splines)
Contrainte : on veut que T(l) soit également l'erreur relative de S_cor par rapport à BT_2796.
Exprimons E_2610(l), non pas en % mais entre 0 et 1 :
E_2610(l) = (Smes(l) - BB_2610(l)) / BB_2610(l)
E_2610(l) = Smes(l) / BB_2610(l) - 1
=> Smes(l) = (E_2610(l) + 1) x BB_2610(l) (Eq. 1)
Soit S(l) le spectre intermédiaire dont l'erreur relative par rapport à BB_2610 est la cible T :
T(l) = S(l) / BB_2610(l) - 1
=> S(l) = (T(l) + 1) x BB_2610(l) (Eq. 2)
On divise (Eq. 2) par (Eq. 1) :
S(l) / Smes(l) = (T(l) + 1) / (E_2610(l) + 1)
S(l) = Smes(l) x (T(l) + 1) / (E_2610(l) + 1)
On pose Correction(l) = (T(l) + 1) / (E_2610(l) + 1) (Eq. 3)
=> S(l) = Smes(l) x Correction(l) (Eq. 4)
La CCT de S(l) n'est pas 2796 K. Elle est proche de 2610 K (proche va dépendre du choix de T).
On veut que S_cor ait aussi T comme erreur relative par rapport à BB_2796 (c'est la contrainte) :
T(l) = S_cor(l) / BB_2796(l) - 1
=> S_cor(l) = (T(l) + 1) x BB_2796(l) (Eq. 5)
On divise (Eq. 5) par (Eq. 1) :
S_cor(l) / Smes(T) = (T(l) + 1) x BB_2796(l) / ((E_2610(l) + 1) x BB_2610(l))
S_cor(l) = Smes(l) x (T(l) + 1) x BB_2796(l) / ((E_2610(l) + 1) x BB_2610(l))
S_cor(l) = Smes(l) x (T(l) + 1) / (E_2610(l) + 1) x BB_2796(l) / BB_2610(l)
Voici donc la formule de correction de Smes :
=> S_cor(l) = Smes(l) x Correction(l) x BB_2796(l) / BB_2610(l) (Eq. 6)
avec Correction(l) donnée par l'Eq. 3.
La CCT de S_cor(l) est proche de 2796 K (proche va dépendre du choix de T).
Nota : le facteur d'ajustement qui permet de passer de S(l) à S_cor(l) est BB_2796(l) / BB_2610(l) puisqu'on a grâce à l'Eq. 4 :
S_cor(l) = S(l) x BB_2796(l) / BB_2610(l)
Modifié en dernier par Emmanuel Piat le 09 févr. 2026, 17:08, modifié 2 fois.
-
Emmanuel Piat
- 34 dB
- Messages : 72
- Enregistré le : 11 janv. 2026, 11:26
Re: Les sondes de calibration
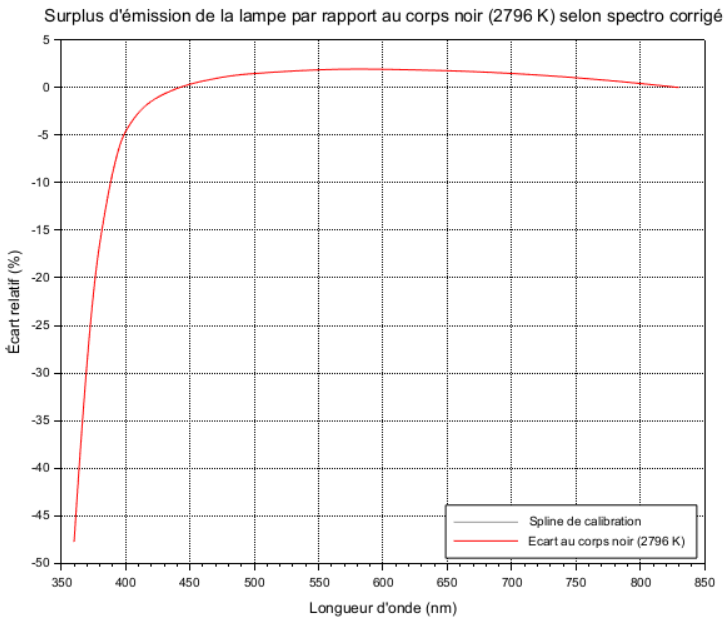
Voici l'écart relatif du spectre corrigé S_cor par rapport à BB_2796. On retrouve bien que c'est la courbe cible tracée avec des splines car les 2 courbes sont superposées.

-
Emmanuel Piat
- 34 dB
- Messages : 72
- Enregistré le : 11 janv. 2026, 11:26
Re: Les sondes de calibration
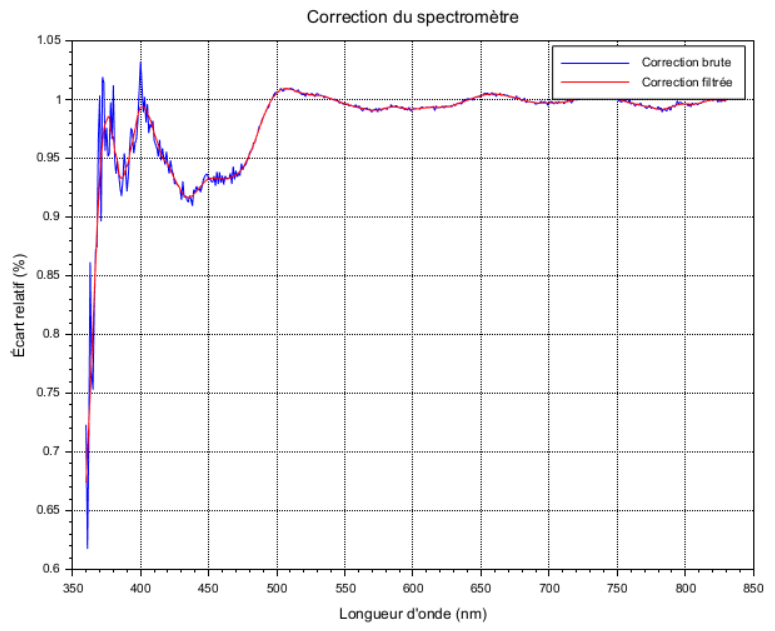
Tiens il n'y a plus de bruit sur l'erreur relative précédente ! Est-ce normal ?
Pour répondre à cette question, voici en bleu la correction totale appliquée à Smes qui est d'après l'Eq. 6 :
Correction(l) x BB_2796(l) / BB_2610(l)
On voit que la courbe bleue est bruitée de manière à compenser très exactement le bruit présent dans Smes. Sauf qu'en pratique le bruit présent dans Smes varie à chaque mesure de nouveau spectre. Donc ce qui a marché une fois ne remarchera pas une 2e fois puisque la correction appliquée est tjrs la même.
En pratique, on évite d'inclure du bruit dans une correction pour ne pas amplifier le bruit déjà présent dans le signal (il peut y avoir des exceptions... Tout dépend du niveau du bruit inclus dans la correction et son impact). Donc ici, on va plutôt utiliser la correction filtrée (en rouge).
Nota : cette correction est un gain G(l). Donc si G(l) = 1 aucune correction n'est appliquée au spectre mesuré Smes(l). On voit ici que la correction varie plus ou moins autour de 1 et elle coupe le signal spectral sous 670 nm.
Pour répondre à cette question, voici en bleu la correction totale appliquée à Smes qui est d'après l'Eq. 6 :
Correction(l) x BB_2796(l) / BB_2610(l)
On voit que la courbe bleue est bruitée de manière à compenser très exactement le bruit présent dans Smes. Sauf qu'en pratique le bruit présent dans Smes varie à chaque mesure de nouveau spectre. Donc ce qui a marché une fois ne remarchera pas une 2e fois puisque la correction appliquée est tjrs la même.
En pratique, on évite d'inclure du bruit dans une correction pour ne pas amplifier le bruit déjà présent dans le signal (il peut y avoir des exceptions... Tout dépend du niveau du bruit inclus dans la correction et son impact). Donc ici, on va plutôt utiliser la correction filtrée (en rouge).
Nota : cette correction est un gain G(l). Donc si G(l) = 1 aucune correction n'est appliquée au spectre mesuré Smes(l). On voit ici que la correction varie plus ou moins autour de 1 et elle coupe le signal spectral sous 670 nm.

Modifié en dernier par Emmanuel Piat le 09 févr. 2026, 17:14, modifié 2 fois.
-
Emmanuel Piat
- 34 dB
- Messages : 72
- Enregistré le : 11 janv. 2026, 11:26
Re: Les sondes de calibration
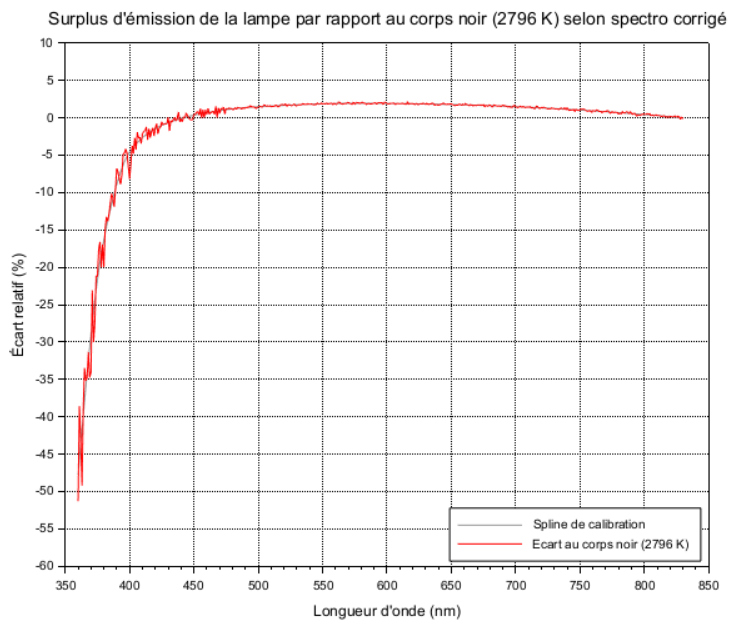
Si on applique la correction filtrée en rouge, on retrouve le bruit sur l'erreur relative et c'est cette situation-là qui est "normale" :

-
Emmanuel Piat
- 34 dB
- Messages : 72
- Enregistré le : 11 janv. 2026, 11:26
Re: Les sondes de calibration
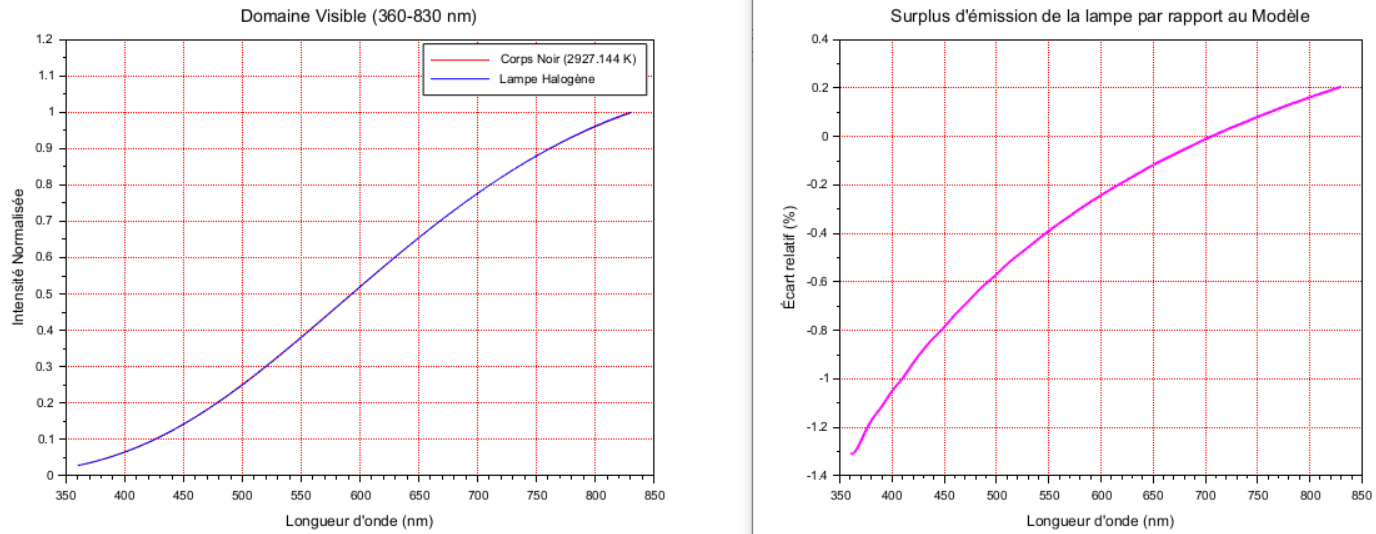
Passons maintenant à la lampe n°1 de Thorlabs. Pour rappel son spectre à une CCT qui vaut 2927.1 K et l'erreur relative entre son spectre et BB_2927 est affichée dans la fig. de droite.

-
Emmanuel Piat
- 34 dB
- Messages : 72
- Enregistré le : 11 janv. 2026, 11:26
Re: Les sondes de calibration
Faut-ll définir une nouvelle cible dans notre contexte de déconvo aveugle ? On ne voit aucun accident sur la forme très régulière de l'erreur relative et cette dernière est faible. Donc, perso, je ne le ferai pas et si la CCT réelle est bien 2796 K (vérifiable avec un colorimètre qui est précis sur les illuminants de type A), je me contenterai juste d'appliquer le facteur d'ajustement des CCT pour déterminer la correction qui sera simplement BB_2796(l) / BB_2927(l).
S_cor(l) = Smes(l) x BB_2796(l) / BB_2927(l)
L'écart relatif du spectre corrigé par rapport cette fois-ci à BB_2796 sera alors tjrs celui de la figure de droite (avec les mêmes valeurs d'erreurs relatives, donc faibles).
Si la CCT réelle de la lampe est xxxx et est différente de 2796, la démarche est strictement la même en remplaçant BB_2796 par BB_xxxx .
S_cor(l) = Smes(l) x BB_2796(l) / BB_2927(l)
L'écart relatif du spectre corrigé par rapport cette fois-ci à BB_2796 sera alors tjrs celui de la figure de droite (avec les mêmes valeurs d'erreurs relatives, donc faibles).
Si la CCT réelle de la lampe est xxxx et est différente de 2796, la démarche est strictement la même en remplaçant BB_2796 par BB_xxxx .
Modifié en dernier par Emmanuel Piat le 09 févr. 2026, 17:04, modifié 3 fois.
-
Emmanuel Piat
- 34 dB
- Messages : 72
- Enregistré le : 11 janv. 2026, 11:26
Re: Les sondes de calibration
Résumé :
dans le contexte de la mesure d'une lampe QTH, le spectre obtenu est sensé être très proche de celui d'un BB si la lampe est correctement mise en oeuvre et peu utilisée. Au fur et à mesure que la lampe vieillit, du tungstène peut se déposer sur les parois de quartz et réduire la transmission dans le bleu.
La différence entre le spectre du BB et le spectre mesuré est induit (i) par l'émissivité du filament de tungstène qui est notamment une fonction de T et de lambda (la géométrie du filament intervient aussi dans la manière dont il rayonne angulairement) et (ii) par tous les défauts de la chaîne acquisition.
Si on veut pouvoir étalonner radiométriquement un spectro en calculant un facteur de correction pour chaque longueur d'onde qui compense les défauts de la chaîne d'acquisition, il faut impérativement disposer d'une lampe étalon dont le spectre est connu et relié au système international d'unités (SI).
Si on peut se contenter d'opérer en relatif (par exemple spectre normalisé à 1 lorsque le projo projette un patch blanc), on peut tenter d'établir une correction en enlevant les défauts présents sur le spectre mesuré. Une première approche très empirique a permis de jeter les bases du calcul de la correction lorsqu'on dispose d'une courbe d'erreur relative E établie grâce à une comparaison avec le spectre normalisé d'un BB à une température T = CCT, avec CCT correspondant au spectre non calibré. Lorsque cette courbe d'erreur relative présente des anomalies "criantes", on peut déjà les supprimer.
Pour aller plus loin dans la démarche de la déconvo semi-aveugle, il faut fournir davantage d'information à l'algo de déconvo. Dans ce cas, on n'a pas d'autres choix que de s'appuyer sur un modèle physique de la lampe QTH pour en déduire quel devrait être son spectre relatif et ainsi affiner la courbe cible.
Il faut que je travaille la question et ça va me prendre un peu de temps.
A suivre ...
dans le contexte de la mesure d'une lampe QTH, le spectre obtenu est sensé être très proche de celui d'un BB si la lampe est correctement mise en oeuvre et peu utilisée. Au fur et à mesure que la lampe vieillit, du tungstène peut se déposer sur les parois de quartz et réduire la transmission dans le bleu.
La différence entre le spectre du BB et le spectre mesuré est induit (i) par l'émissivité du filament de tungstène qui est notamment une fonction de T et de lambda (la géométrie du filament intervient aussi dans la manière dont il rayonne angulairement) et (ii) par tous les défauts de la chaîne acquisition.
Si on veut pouvoir étalonner radiométriquement un spectro en calculant un facteur de correction pour chaque longueur d'onde qui compense les défauts de la chaîne d'acquisition, il faut impérativement disposer d'une lampe étalon dont le spectre est connu et relié au système international d'unités (SI).
Si on peut se contenter d'opérer en relatif (par exemple spectre normalisé à 1 lorsque le projo projette un patch blanc), on peut tenter d'établir une correction en enlevant les défauts présents sur le spectre mesuré. Une première approche très empirique a permis de jeter les bases du calcul de la correction lorsqu'on dispose d'une courbe d'erreur relative E établie grâce à une comparaison avec le spectre normalisé d'un BB à une température T = CCT, avec CCT correspondant au spectre non calibré. Lorsque cette courbe d'erreur relative présente des anomalies "criantes", on peut déjà les supprimer.
Pour aller plus loin dans la démarche de la déconvo semi-aveugle, il faut fournir davantage d'information à l'algo de déconvo. Dans ce cas, on n'a pas d'autres choix que de s'appuyer sur un modèle physique de la lampe QTH pour en déduire quel devrait être son spectre relatif et ainsi affiner la courbe cible.
Il faut que je travaille la question et ça va me prendre un peu de temps.
A suivre ...
Modifié en dernier par Emmanuel Piat le 10 févr. 2026, 16:33, modifié 1 fois.
Re: Les sondes de calibration
Petite correction, que me répète THXRD et qui a fini par me rentrer dans le crâne : ma mère ne voit pas l'ultraviolet, mais son opération lui a redonné une vision dans l'extrémité violette du spectre proche de celle d'une personne de 20 ans (source : https://pubmed.ncbi.nlm.nih.gov/8109464/), bien supérieure à la mienne.
Re: Les sondes de calibration
il faut savoir que l’opacification du cristallin commence en fait assez tôt en moyenne ( vers 40/55 ans )
mais cela évolue très lentement ..voir dans qqs rares cas ne va jamais complètement au bout..
en moyenne apres 65/70 ans l’opacification augmente plus vite et peut même varier de 25/ä 40 % sur 2 ans
on peut donc dire que la vision coté spectral bouge des 40 /50 ans ..
et qu’au delã de 65/70 ..elle n’est plus du tout celle de 20 ans ou moins ..
l’opération et le remplacement par un insert est une opération relativement banale de nos jours qui dure entre 15 et 20 mn et permet de retrouver une vision normale ( autant en lumière qu’en spectre )
il existe plein de type de cristallin « artificiel » et il est bon de bien se documenter avant
et comme souvent ( surtout en optique ) les plus simples sont ceux qui donne le plus de lumière et le plus large spectre ..
aucune magie …comme toujours
et idealement il faudra des lunettes ( car si on peut récupérer le spectre et la lumiere , l’insert n.est pas adaptatif ( vivant ) en live comme le vrai cristallin
et l’usage de multi focaux ou focales variables entraîne bien plus de problèmes que d’avantages ..( et fait perdre de la lumière )
le plus spectaculaire apres l’operation du 1 er oeil est la découverte que l’on avait en fait perdu trës largement le spectre d.origine ( l’écart est énorme vers T° chaud et jaunâtre ) ..
en gros apres une opération appellé balance avec monofocaux on récupère 100 % de la lumière et spectre que l’on avait dans son enfance
et pour la vision , des lunettes avec correction inversées permettent 10 à 12 eme sans problemes et avec une infime perte de lumière et quasi 0 sur le spectre si bon choix de la techno des verres ( et c’est définitif )
Roland
mais cela évolue très lentement ..voir dans qqs rares cas ne va jamais complètement au bout..
en moyenne apres 65/70 ans l’opacification augmente plus vite et peut même varier de 25/ä 40 % sur 2 ans
on peut donc dire que la vision coté spectral bouge des 40 /50 ans ..
et qu’au delã de 65/70 ..elle n’est plus du tout celle de 20 ans ou moins ..
l’opération et le remplacement par un insert est une opération relativement banale de nos jours qui dure entre 15 et 20 mn et permet de retrouver une vision normale ( autant en lumière qu’en spectre )
il existe plein de type de cristallin « artificiel » et il est bon de bien se documenter avant
et comme souvent ( surtout en optique ) les plus simples sont ceux qui donne le plus de lumière et le plus large spectre ..
aucune magie …comme toujours
et idealement il faudra des lunettes ( car si on peut récupérer le spectre et la lumiere , l’insert n.est pas adaptatif ( vivant ) en live comme le vrai cristallin
et l’usage de multi focaux ou focales variables entraîne bien plus de problèmes que d’avantages ..( et fait perdre de la lumière )
le plus spectaculaire apres l’operation du 1 er oeil est la découverte que l’on avait en fait perdu trës largement le spectre d.origine ( l’écart est énorme vers T° chaud et jaunâtre ) ..
en gros apres une opération appellé balance avec monofocaux on récupère 100 % de la lumière et spectre que l’on avait dans son enfance
et pour la vision , des lunettes avec correction inversées permettent 10 à 12 eme sans problemes et avec une infime perte de lumière et quasi 0 sur le spectre si bon choix de la techno des verres ( et c’est définitif )
Roland
-
Emmanuel Piat
- 34 dB
- Messages : 72
- Enregistré le : 11 janv. 2026, 11:26
Re: Les sondes de calibration
Le code que j'utilisais pour calculer la CCT reposait sur la formule approchée de McCamy qui a l'avantage d'être simple. Je me suis rendu compte qu'elle produisait qd même une petite erreur sur les illuminants de type A qui nous intéressent ici. Désormais, j'utilise une implémentation de la méthode officielle utilisée par le NIST qui repose sur un algo de recherche itérative (méthode OHNO). C'est très précis et j'ai même la distance d_uv au lieu Planckien des coordonnées chromatiques du spectre (d_uv est exprimée dans l'espace CIE 1960 uv qui est perceptuellement uniforme). La valeur de d_uv permet de quantifier numériquement si le spectre mesuré est proche ou pas de celui d'un corps noir. Ce n'est pas un code simple à écrire si on veut avoir une bonne vitesse d'exécution. J'ai donc utilisé une IA pour optimiser son implémentation sous Scilab en remplaçant la méthode de recherche standard par une recherche dichotomique non-linéaire basée sur des exponentielles. Ca permet de gagner un ratio x600 sur le temps de calcul. J'ai vérifié que ça fonctionnait bien avec des données connues de correspondance (x,y) <-> CCT.
Je mettrai bientôt à disposition mon code de calcul sous Scilab pour vous permettre de jouer avec.
Je mettrai bientôt à disposition mon code de calcul sous Scilab pour vous permettre de jouer avec.
Modifié en dernier par Emmanuel Piat le 10 févr. 2026, 20:55, modifié 1 fois.
-
Emmanuel Piat
- 34 dB
- Messages : 72
- Enregistré le : 11 janv. 2026, 11:26
Re: Les sondes de calibration
Le code Scilab qui affiche tous les graphiques concernant la lampe n°2 (Thorlabs) lit 2 fichiers externes qu'il faut créer :
(1) les données spectrales fournies par Thorlabs que j'ai exporté depuis un fichier Excel.
(2) la table des colors matching functions (x_barre(lambda), y_barre(lambda), z_barre(lambda) de l'Observateur Standard CIE 1931 que j'ai récupéré sur le site officiel de la CIE. Cette table contient la valeur de ces fonctions entre 360 nm et 830 nm par pas de 1 nm. Elle est dispo ici :
https://www.cie.co.at/data-tables
(1) Fichier "SLS201_Spectrum_Model2_VIS.txt"
(2) Fichier "ciexyz31.txt"
(1) les données spectrales fournies par Thorlabs que j'ai exporté depuis un fichier Excel.
(2) la table des colors matching functions (x_barre(lambda), y_barre(lambda), z_barre(lambda) de l'Observateur Standard CIE 1931 que j'ai récupéré sur le site officiel de la CIE. Cette table contient la valeur de ces fonctions entre 360 nm et 830 nm par pas de 1 nm. Elle est dispo ici :
https://www.cie.co.at/data-tables
(1) Fichier "SLS201_Spectrum_Model2_VIS.txt"
Code : Tout sélectionner
360 0.006502006
361 0.008142993
362 0.007515264
363 0.006630921
364 0.007912869
365 0.008552697
366 0.008283766
367 0.008271222
368 0.008688231
369 0.008281525
370 0.008396103
371 0.009870863
372 0.009102076
373 0.00957077
374 0.010615491
375 0.010856352
376 0.011605264
377 0.012060881
378 0.011980271
379 0.01284087
380 0.012706613
381 0.014022739
382 0.014713811
383 0.015043662
384 0.015753374
385 0.016475783
386 0.017147688
387 0.017430827
388 0.017571311
389 0.018357315
390 0.019336767
391 0.019633653
392 0.019737163
393 0.019944594
394 0.020581878
395 0.021564338
396 0.021955189
397 0.022444104
398 0.022671815
399 0.022667437
400 0.022681874
401 0.023735632
402 0.024846396
403 0.025115101
404 0.026282018
405 0.026485213
406 0.02779398
407 0.028221855
408 0.028946381
409 0.029433505
410 0.030616687
411 0.031407242
412 0.032210279
413 0.033167424
414 0.033387673
415 0.034737396
416 0.035091442
417 0.036158411
418 0.037126363
419 0.037458369
420 0.038683993
421 0.039782607
422 0.040101802
423 0.041286556
424 0.042248437
425 0.043484013
426 0.044238015
427 0.045246178
428 0.046154026
429 0.047151366
430 0.048559845
431 0.048632902
432 0.050296734
433 0.051145513
434 0.052282578
435 0.053384235
436 0.05401612
437 0.055187708
438 0.05654005
439 0.056696553
440 0.057841517
441 0.058541369
442 0.059815223
443 0.060663706
444 0.062002682
445 0.062732167
446 0.063457337
447 0.064317596
448 0.065253186
449 0.06634174
450 0.067808311
451 0.068847211
452 0.070166156
453 0.07134577
454 0.072110102
455 0.073932235
456 0.074153587
457 0.076186823
458 0.076551785
459 0.078517414
460 0.079229805
461 0.081121537
462 0.081732178
463 0.083126559
464 0.084437154
465 0.085734138
466 0.086593436
467 0.08875323
468 0.088660836
469 0.091039909
470 0.09163175
471 0.093505033
472 0.094629094
473 0.096113177
474 0.096444645
475 0.09837209
476 0.099427563
477 0.100754328
478 0.101783638
479 0.102980224
480 0.103891399
481 0.105074362
482 0.106390888
483 0.107231377
484 0.108617053
485 0.109559028
486 0.110656463
487 0.111485522
488 0.112820688
489 0.113811814
490 0.114982639
491 0.116146956
492 0.117386831
493 0.118535845
494 0.119991896
495 0.120934952
496 0.122279449
497 0.123492952
498 0.124667359
499 0.125970476
500 0.1275886
501 0.129036839
502 0.130498187
503 0.131749112
504 0.133634427
505 0.135253521
506 0.13652003
507 0.138263492
508 0.139749204
509 0.141524929
510 0.142961037
511 0.144721185
512 0.146401531
513 0.148305911
514 0.150098929
515 0.151555992
516 0.153295258
517 0.155296546
518 0.157270354
519 0.158996525
520 0.160653312
521 0.162767055
522 0.163990653
523 0.165965851
524 0.167907166
525 0.169486018
526 0.171199091
527 0.173288138
528 0.175296164
529 0.176642166
530 0.178461221
531 0.180604004
532 0.182392103
533 0.184308553
534 0.186302234
535 0.188420581
536 0.190048044
537 0.192128943
538 0.194027795
539 0.196217371
540 0.197958807
541 0.200196397
542 0.201982795
543 0.203950745
544 0.206106176
545 0.207999421
546 0.210557108
547 0.212281417
548 0.214414793
549 0.216719938
550 0.218427248
551 0.220821054
552 0.222527105
553 0.225093471
554 0.22684105
555 0.229016858
556 0.231225603
557 0.233493097
558 0.235007944
559 0.237721773
560 0.239425442
561 0.241634377
562 0.244327554
563 0.24675076
564 0.248213014
565 0.250462579
566 0.252350056
567 0.254922724
568 0.256838948
569 0.259491981
570 0.261818167
571 0.263491618
572 0.265627229
573 0.267449175
574 0.270487093
575 0.271730727
576 0.27445011
577 0.276614329
578 0.278478832
579 0.280445628
580 0.282785753
581 0.285198904
582 0.286813706
583 0.289195956
584 0.290581675
585 0.293343744
586 0.295465261
587 0.297539449
588 0.299731336
589 0.302330713
590 0.304674982
591 0.307179188
592 0.308796987
593 0.311740473
594 0.314238223
595 0.316285352
596 0.318906999
597 0.320334848
598 0.323507161
599 0.325829739
600 0.327550525
601 0.329813479
602 0.332006725
603 0.334509091
604 0.336578264
605 0.339274034
606 0.3408171
607 0.343061163
608 0.345686353
609 0.347918815
610 0.350015431
611 0.352491404
612 0.354816604
613 0.356885864
614 0.359255544
615 0.361294962
616 0.364996613
617 0.365807896
618 0.368822974
619 0.37099463
620 0.373334678
621 0.375486232
622 0.377481055
623 0.380537826
624 0.382113395
625 0.384566943
626 0.387164808
627 0.389215777
628 0.391795334
629 0.393986766
630 0.395540751
631 0.398574122
632 0.399993937
633 0.402427749
634 0.404654082
635 0.407218581
636 0.409437093
637 0.410384943
638 0.413263558
639 0.41518729
640 0.417046559
641 0.419444441
642 0.421991841
643 0.424299627
644 0.427041272
645 0.428466958
646 0.430556287
647 0.432897214
648 0.43499052
649 0.437564106
650 0.439377166
651 0.441733635
652 0.443234605
653 0.445481352
654 0.447945084
655 0.450094964
656 0.453142863
657 0.455168056
658 0.456704133
659 0.460181803
660 0.46173428
661 0.465344222
662 0.466702347
663 0.469269729
664 0.470925154
665 0.474352586
666 0.476163021
667 0.478353115
668 0.481306895
669 0.483288179
670 0.486050455
671 0.488823644
672 0.490865374
673 0.493749382
674 0.495624998
675 0.498941229
676 0.499697016
677 0.50346027
678 0.505085283
679 0.508329473
680 0.51118869
681 0.512905452
682 0.514520357
683 0.518771284
684 0.520804155
685 0.522909127
686 0.525137976
687 0.52792723
688 0.529919553
689 0.532481667
690 0.535647997
691 0.53754649
692 0.539748534
693 0.541908976
694 0.543251278
695 0.546550114
696 0.548064343
697 0.550312632
698 0.55317043
699 0.55654075
700 0.557659957
701 0.559339678
702 0.561409978
703 0.564682078
704 0.566908426
705 0.568230312
706 0.571532846
707 0.572488752
708 0.575375665
709 0.57754313
710 0.579503671
711 0.582626093
712 0.583364137
713 0.585955598
714 0.587080079
715 0.58889986
716 0.593170158
717 0.594865545
718 0.595805506
719 0.597358117
720 0.600506582
721 0.601591992
722 0.604672885
723 0.605673796
724 0.607623818
725 0.608532269
726 0.611509539
727 0.612895544
728 0.616199599
729 0.617284944
730 0.619932433
731 0.621177043
732 0.624086089
733 0.625182898
734 0.627695623
735 0.630632486
736 0.63290034
737 0.634036733
738 0.637764967
739 0.637860354
740 0.642175367
741 0.642267098
742 0.644168263
743 0.646697961
744 0.648962812
745 0.651687851
746 0.651849385
747 0.65642892
748 0.657475727
749 0.65978303
750 0.662708806
751 0.665411298
752 0.667623885
753 0.670250156
754 0.671340316
755 0.673422757
756 0.674793313
757 0.678261267
758 0.679968722
759 0.680824218
760 0.685203575
761 0.686241973
762 0.688713098
763 0.692321428
764 0.693573206
765 0.694648545
766 0.697615291
767 0.697951684
768 0.701598488
769 0.703604704
770 0.705866748
771 0.708806751
772 0.710790713
773 0.711031517
774 0.712744746
775 0.716672419
776 0.71742105
777 0.720396997
778 0.721997386
779 0.724661481
780 0.724527819
781 0.727842133
782 0.728867024
783 0.733413915
784 0.733136573
785 0.735367395
786 0.738391683
787 0.739215006
788 0.739212229
789 0.743423728
790 0.742820834
791 0.743401104
792 0.746499444
793 0.746899236
794 0.74602555
795 0.749611115
796 0.750118832
797 0.752348574
798 0.754637853
799 0.756763578
800 0.75873556
801 0.759609842
802 0.76311728
803 0.763578329
804 0.766776161
805 0.765853998
806 0.769060204
807 0.769666715
808 0.770961469
809 0.773873249
810 0.774098532
811 0.77634794
812 0.777076237
813 0.777885076
814 0.779237658
815 0.781542683
816 0.782143353
817 0.78269268
818 0.784886878
819 0.785498556
820 0.788688957
821 0.789215411
822 0.790848025
823 0.792588786
824 0.795529745
825 0.79522041
826 0.798370372
827 0.799528808
828 0.798479283
829 0.802799046
830 0.802329233
Code : Tout sélectionner
360, 0.000129900000, 0.000003917000, 0.000606100000
361, 0.000145847000, 0.000004393581, 0.000680879200
362, 0.000163802100, 0.000004929604, 0.000765145600
363, 0.000184003700, 0.000005532136, 0.000860012400
364, 0.000206690200, 0.000006208245, 0.000966592800
365, 0.000232100000, 0.000006965000, 0.001086000000
366, 0.000260728000, 0.000007813219, 0.001220586000
367, 0.000293075000, 0.000008767336, 0.001372729000
368, 0.000329388000, 0.000009839844, 0.001543579000
369, 0.000369914000, 0.000011043230, 0.001734286000
370, 0.000414900000, 0.000012390000, 0.001946000000
371, 0.000464158700, 0.000013886410, 0.002177777000
372, 0.000518986000, 0.000015557280, 0.002435809000
373, 0.000581854000, 0.000017442960, 0.002731953000
374, 0.000655234700, 0.000019583750, 0.003078064000
375, 0.000741600000, 0.000022020000, 0.003486000000
376, 0.000845029600, 0.000024839650, 0.003975227000
377, 0.000964526800, 0.000028041260, 0.004540880000
378, 0.001094949000, 0.000031531040, 0.005158320000
379, 0.001231154000, 0.000035215210, 0.005802907000
380, 0.001368000000, 0.000039000000, 0.006450001000
381, 0.001502050000, 0.000042826400, 0.007083216000
382, 0.001642328000, 0.000046914600, 0.007745488000
383, 0.001802382000, 0.000051589600, 0.008501152000
384, 0.001995757000, 0.000057176400, 0.009414544000
385, 0.002236000000, 0.000064000000, 0.010549990000
386, 0.002535385000, 0.000072344210, 0.011965800000
387, 0.002892603000, 0.000082212240, 0.013655870000
388, 0.003300829000, 0.000093508160, 0.015588050000
389, 0.003753236000, 0.000106136100, 0.017730150000
390, 0.004243000000, 0.000120000000, 0.020050010000
391, 0.004762389000, 0.000134984000, 0.022511360000
392, 0.005330048000, 0.000151492000, 0.025202880000
393, 0.005978712000, 0.000170208000, 0.028279720000
394, 0.006741117000, 0.000191816000, 0.031897040000
395, 0.007650000000, 0.000217000000, 0.036210000000
396, 0.008751373000, 0.000246906700, 0.041437710000
397, 0.010028880000, 0.000281240000, 0.047503720000
398, 0.011421700000, 0.000318520000, 0.054119880000
399, 0.012869010000, 0.000357266700, 0.060998030000
400, 0.014310000000, 0.000396000000, 0.067850010000
401, 0.015704430000, 0.000433714700, 0.074486320000
402, 0.017147440000, 0.000473024000, 0.081361560000
403, 0.018781220000, 0.000517876000, 0.089153640000
404, 0.020748010000, 0.000572218700, 0.098540480000
405, 0.023190000000, 0.000640000000, 0.110200000000
406, 0.026207360000, 0.000724560000, 0.124613300000
407, 0.029782480000, 0.000825500000, 0.141701700000
408, 0.033880920000, 0.000941160000, 0.161303500000
409, 0.038468240000, 0.001069880000, 0.183256800000
410, 0.043510000000, 0.001210000000, 0.207400000000
411, 0.048995600000, 0.001362091000, 0.233692100000
412, 0.055022600000, 0.001530752000, 0.262611400000
413, 0.061718800000, 0.001720368000, 0.294774600000
414, 0.069212000000, 0.001935323000, 0.330798500000
415, 0.077630000000, 0.002180000000, 0.371300000000
416, 0.086958110000, 0.002454800000, 0.416209100000
417, 0.097176720000, 0.002764000000, 0.465464200000
418, 0.108406300000, 0.003117800000, 0.519694800000
419, 0.120767200000, 0.003526400000, 0.579530300000
420, 0.134380000000, 0.004000000000, 0.645600000000
421, 0.149358200000, 0.004546240000, 0.718483800000
422, 0.165395700000, 0.005159320000, 0.796713300000
423, 0.181983100000, 0.005829280000, 0.877845900000
424, 0.198611000000, 0.006546160000, 0.959439000000
425, 0.214770000000, 0.007300000000, 1.039050100000
426, 0.230186800000, 0.008086507000, 1.115367300000
427, 0.244879700000, 0.008908720000, 1.188497100000
428, 0.258777300000, 0.009767680000, 1.258123300000
429, 0.271807900000, 0.010664430000, 1.323929600000
430, 0.283900000000, 0.011600000000, 1.385600000000
431, 0.294943800000, 0.012573170000, 1.442635200000
432, 0.304896500000, 0.013582720000, 1.494803500000
433, 0.313787300000, 0.014629680000, 1.542190300000
434, 0.321645400000, 0.015715090000, 1.584880700000
435, 0.328500000000, 0.016840000000, 1.622960000000
436, 0.334351300000, 0.018007360000, 1.656404800000
437, 0.339210100000, 0.019214480000, 1.685295900000
438, 0.343121300000, 0.020453920000, 1.709874500000
439, 0.346129600000, 0.021718240000, 1.730382100000
440, 0.348280000000, 0.023000000000, 1.747060000000
441, 0.349599900000, 0.024294610000, 1.760044600000
442, 0.350147400000, 0.025610240000, 1.769623300000
443, 0.350013000000, 0.026958570000, 1.776263700000
444, 0.349287000000, 0.028351250000, 1.780433400000
445, 0.348060000000, 0.029800000000, 1.782600000000
446, 0.346373300000, 0.031310830000, 1.782968200000
447, 0.344262400000, 0.032883680000, 1.781699800000
448, 0.341808800000, 0.034521120000, 1.779198200000
449, 0.339094100000, 0.036225710000, 1.775867100000
450, 0.336200000000, 0.038000000000, 1.772110000000
451, 0.333197700000, 0.039846670000, 1.768258900000
452, 0.330041100000, 0.041768000000, 1.764039000000
453, 0.326635700000, 0.043766000000, 1.758943800000
454, 0.322886800000, 0.045842670000, 1.752466300000
455, 0.318700000000, 0.048000000000, 1.744100000000
456, 0.314025100000, 0.050243680000, 1.733559500000
457, 0.308884000000, 0.052573040000, 1.720858100000
458, 0.303290400000, 0.054980560000, 1.705936900000
459, 0.297257900000, 0.057458720000, 1.688737200000
460, 0.290800000000, 0.060000000000, 1.669200000000
461, 0.283970100000, 0.062601970000, 1.647528700000
462, 0.276721400000, 0.065277520000, 1.623412700000
463, 0.268917800000, 0.068042080000, 1.596022300000
464, 0.260422700000, 0.070911090000, 1.564528000000
465, 0.251100000000, 0.073900000000, 1.528100000000
466, 0.240847500000, 0.077016000000, 1.486111400000
467, 0.229851200000, 0.080266400000, 1.439521500000
468, 0.218407200000, 0.083666800000, 1.389879900000
469, 0.206811500000, 0.087232800000, 1.338736200000
470, 0.195360000000, 0.090980000000, 1.287640000000
471, 0.184213600000, 0.094917550000, 1.237422300000
472, 0.173327300000, 0.099045840000, 1.187824300000
473, 0.162688100000, 0.103367400000, 1.138761100000
474, 0.152283300000, 0.107884600000, 1.090148000000
475, 0.142100000000, 0.112600000000, 1.041900000000
476, 0.132178600000, 0.117532000000, 0.994197600000
477, 0.122569600000, 0.122674400000, 0.947347300000
478, 0.113275200000, 0.127992800000, 0.901453100000
479, 0.104297900000, 0.133452800000, 0.856619300000
480, 0.095640000000, 0.139020000000, 0.812950100000
481, 0.087299550000, 0.144676400000, 0.770517300000
482, 0.079308040000, 0.150469300000, 0.729444800000
483, 0.071717760000, 0.156461900000, 0.689913600000
484, 0.064580990000, 0.162717700000, 0.652104900000
485, 0.057950010000, 0.169300000000, 0.616200000000
486, 0.051862110000, 0.176243100000, 0.582328600000
487, 0.046281520000, 0.183558100000, 0.550416200000
488, 0.041150880000, 0.191273500000, 0.520337600000
489, 0.036412830000, 0.199418000000, 0.491967300000
490, 0.032010000000, 0.208020000000, 0.465180000000
491, 0.027917200000, 0.217119900000, 0.439924600000
492, 0.024144400000, 0.226734500000, 0.416183600000
493, 0.020687000000, 0.236857100000, 0.393882200000
494, 0.017540400000, 0.247481200000, 0.372945900000
495, 0.014700000000, 0.258600000000, 0.353300000000
496, 0.012161790000, 0.270184900000, 0.334857800000
497, 0.009919960000, 0.282293900000, 0.317552100000
498, 0.007967240000, 0.295050500000, 0.301337500000
499, 0.006296346000, 0.308578000000, 0.286168600000
500, 0.004900000000, 0.323000000000, 0.272000000000
501, 0.003777173000, 0.338402100000, 0.258817100000
502, 0.002945320000, 0.354685800000, 0.246483800000
503, 0.002424880000, 0.371698600000, 0.234771800000
504, 0.002236293000, 0.389287500000, 0.223453300000
505, 0.002400000000, 0.407300000000, 0.212300000000
506, 0.002925520000, 0.425629900000, 0.201169200000
507, 0.003836560000, 0.444309600000, 0.190119600000
508, 0.005174840000, 0.463394400000, 0.179225400000
509, 0.006982080000, 0.482939500000, 0.168560800000
510, 0.009300000000, 0.503000000000, 0.158200000000
511, 0.012149490000, 0.523569300000, 0.148138300000
512, 0.015535880000, 0.544512000000, 0.138375800000
513, 0.019477520000, 0.565690000000, 0.128994200000
514, 0.023992770000, 0.586965300000, 0.120075100000
515, 0.029100000000, 0.608200000000, 0.111700000000
516, 0.034814850000, 0.629345600000, 0.103904800000
517, 0.041120160000, 0.650306800000, 0.096667480000
518, 0.047985040000, 0.670875200000, 0.089982720000
519, 0.055378610000, 0.690842400000, 0.083845310000
520, 0.063270000000, 0.710000000000, 0.078249990000
521, 0.071635010000, 0.728185200000, 0.073208990000
522, 0.080462240000, 0.745463600000, 0.068678160000
523, 0.089739960000, 0.761969400000, 0.064567840000
524, 0.099456450000, 0.777836800000, 0.060788350000
525, 0.109600000000, 0.793200000000, 0.057250010000
526, 0.120167400000, 0.808110400000, 0.053904350000
527, 0.131114500000, 0.822496200000, 0.050746640000
528, 0.142367900000, 0.836306800000, 0.047752760000
529, 0.153854200000, 0.849491600000, 0.044898590000
530, 0.165500000000, 0.862000000000, 0.042160000000
531, 0.177257100000, 0.873810800000, 0.039507280000
532, 0.189140000000, 0.884962400000, 0.036935640000
533, 0.201169400000, 0.895493600000, 0.034458360000
534, 0.213365800000, 0.905443200000, 0.032088720000
535, 0.225749900000, 0.914850100000, 0.029840000000
536, 0.238320900000, 0.923734800000, 0.027711810000
537, 0.251066800000, 0.932092400000, 0.025694440000
538, 0.263992200000, 0.939922600000, 0.023787160000
539, 0.277101700000, 0.947225200000, 0.021989250000
540, 0.290400000000, 0.954000000000, 0.020300000000
541, 0.303891200000, 0.960256100000, 0.018718050000
542, 0.317572600000, 0.966007400000, 0.017240360000
543, 0.331438400000, 0.971260600000, 0.015863640000
544, 0.345482800000, 0.976022500000, 0.014584610000
545, 0.359700000000, 0.980300000000, 0.013400000000
546, 0.374083900000, 0.984092400000, 0.012307230000
547, 0.388639600000, 0.987418200000, 0.011301880000
548, 0.403378400000, 0.990312800000, 0.010377920000
549, 0.418311500000, 0.992811600000, 0.009529306000
550, 0.433449900000, 0.994950100000, 0.008749999000
551, 0.448795300000, 0.996710800000, 0.008035200000
552, 0.464336000000, 0.998098300000, 0.007381600000
553, 0.480064000000, 0.999112000000, 0.006785400000
554, 0.495971300000, 0.999748200000, 0.006242800000
555, 0.512050100000, 1.000000000000, 0.005749999000
556, 0.528295900000, 0.999856700000, 0.005303600000
557, 0.544691600000, 0.999304600000, 0.004899800000
558, 0.561209400000, 0.998325500000, 0.004534200000
559, 0.577821500000, 0.996898700000, 0.004202400000
560, 0.594500000000, 0.995000000000, 0.003900000000
561, 0.611220900000, 0.992600500000, 0.003623200000
562, 0.627975800000, 0.989742600000, 0.003370600000
563, 0.644760200000, 0.986444400000, 0.003141400000
564, 0.661569700000, 0.982724100000, 0.002934800000
565, 0.678400000000, 0.978600000000, 0.002749999000
566, 0.695239200000, 0.974083700000, 0.002585200000
567, 0.712058600000, 0.969171200000, 0.002438600000
568, 0.728828400000, 0.963856800000, 0.002309400000
569, 0.745518800000, 0.958134900000, 0.002196800000
570, 0.762100000000, 0.952000000000, 0.002100000000
571, 0.778543200000, 0.945450400000, 0.002017733000
572, 0.794825600000, 0.938499200000, 0.001948200000
573, 0.810926400000, 0.931162800000, 0.001889800000
574, 0.826824800000, 0.923457600000, 0.001840933000
575, 0.842500000000, 0.915400000000, 0.001800000000
576, 0.857932500000, 0.907006400000, 0.001766267000
577, 0.873081600000, 0.898277200000, 0.001737800000
578, 0.887894400000, 0.889204800000, 0.001711200000
579, 0.902318100000, 0.879781600000, 0.001683067000
580, 0.916300000000, 0.870000000000, 0.001650001000
581, 0.929799500000, 0.859861300000, 0.001610133000
582, 0.942798400000, 0.849392000000, 0.001564400000
583, 0.955277600000, 0.838622000000, 0.001513600000
584, 0.967217900000, 0.827581300000, 0.001458533000
585, 0.978600000000, 0.816300000000, 0.001400000000
586, 0.989385600000, 0.804794700000, 0.001336667000
587, 0.999548800000, 0.793082000000, 0.001270000000
588, 1.009089200000, 0.781192000000, 0.001205000000
589, 1.018006400000, 0.769154700000, 0.001146667000
590, 1.026300000000, 0.757000000000, 0.001100000000
591, 1.033982700000, 0.744754100000, 0.001068800000
592, 1.040986000000, 0.732422400000, 0.001049400000
593, 1.047188000000, 0.720003600000, 0.001035600000
594, 1.052466700000, 0.707496500000, 0.001021200000
595, 1.056700000000, 0.694900000000, 0.001000000000
596, 1.059794400000, 0.682219200000, 0.000968640000
597, 1.061799200000, 0.669471600000, 0.000929920000
598, 1.062806800000, 0.656674400000, 0.000886880000
599, 1.062909600000, 0.643844800000, 0.000842560000
600, 1.062200000000, 0.631000000000, 0.000800000000
601, 1.060735200000, 0.618155500000, 0.000760960000
602, 1.058443600000, 0.605314400000, 0.000723680000
603, 1.055224400000, 0.592475600000, 0.000685920000
604, 1.050976800000, 0.579637900000, 0.000645440000
605, 1.045600000000, 0.566800000000, 0.000600000000
606, 1.039036900000, 0.553961100000, 0.000547866700
607, 1.031360800000, 0.541137200000, 0.000491600000
608, 1.022666200000, 0.528352800000, 0.000435400000
609, 1.013047700000, 0.515632300000, 0.000383466700
610, 1.002600000000, 0.503000000000, 0.000340000000
611, 0.991367500000, 0.490468800000, 0.000307253300
612, 0.979331400000, 0.478030400000, 0.000283160000
613, 0.966491600000, 0.465677600000, 0.000265440000
614, 0.952847900000, 0.453403200000, 0.000251813300
615, 0.938400000000, 0.441200000000, 0.000240000000
616, 0.923194000000, 0.429080000000, 0.000229546700
617, 0.907244000000, 0.417036000000, 0.000220640000
618, 0.890502000000, 0.405032000000, 0.000211960000
619, 0.872920000000, 0.393032000000, 0.000202186700
620, 0.854449900000, 0.381000000000, 0.000190000000
621, 0.835084000000, 0.368918400000, 0.000174213300
622, 0.814946000000, 0.356827200000, 0.000155640000
623, 0.794186000000, 0.344776800000, 0.000135960000
624, 0.772954000000, 0.332817600000, 0.000116853300
625, 0.751400000000, 0.321000000000, 0.000100000000
626, 0.729583600000, 0.309338100000, 0.000086133330
627, 0.707588800000, 0.297850400000, 0.000074600000
628, 0.685602200000, 0.286593600000, 0.000065000000
629, 0.663810400000, 0.275624500000, 0.000056933330
630, 0.642400000000, 0.265000000000, 0.000049999990
631, 0.621514900000, 0.254763200000, 0.000044160000
632, 0.601113800000, 0.244889600000, 0.000039480000
633, 0.581105200000, 0.235334400000, 0.000035720000
634, 0.561397700000, 0.226052800000, 0.000032640000
635, 0.541900000000, 0.217000000000, 0.000030000000
636, 0.522599500000, 0.208161600000, 0.000027653330
637, 0.503546400000, 0.199548800000, 0.000025560000
638, 0.484743600000, 0.191155200000, 0.000023640000
639, 0.466193900000, 0.182974400000, 0.000021813330
640, 0.447900000000, 0.175000000000, 0.000020000000
641, 0.429861300000, 0.167223500000, 0.000018133330
642, 0.412098000000, 0.159646400000, 0.000016200000
643, 0.394644000000, 0.152277600000, 0.000014200000
644, 0.377533300000, 0.145125900000, 0.000012133330
645, 0.360800000000, 0.138200000000, 0.000010000000
646, 0.344456300000, 0.131500300000, 0.000007733333
647, 0.328516800000, 0.125024800000, 0.000005400000
648, 0.313019200000, 0.118779200000, 0.000003200000
649, 0.298001100000, 0.112769100000, 0.000001333333
650, 0.283500000000, 0.107000000000, 0.000000000000
651, 0.269544800000, 0.101476200000, 0.000000000000
652, 0.256118400000, 0.096188640000, 0.000000000000
653, 0.243189600000, 0.091122960000, 0.000000000000
654, 0.230727200000, 0.086264850000, 0.000000000000
655, 0.218700000000, 0.081600000000, 0.000000000000
656, 0.207097100000, 0.077120640000, 0.000000000000
657, 0.195923200000, 0.072825520000, 0.000000000000
658, 0.185170800000, 0.068710080000, 0.000000000000
659, 0.174832300000, 0.064769760000, 0.000000000000
660, 0.164900000000, 0.061000000000, 0.000000000000
661, 0.155366700000, 0.057396210000, 0.000000000000
662, 0.146230000000, 0.053955040000, 0.000000000000
663, 0.137490000000, 0.050673760000, 0.000000000000
664, 0.129146700000, 0.047549650000, 0.000000000000
665, 0.121200000000, 0.044580000000, 0.000000000000
666, 0.113639700000, 0.041758720000, 0.000000000000
667, 0.106465000000, 0.039084960000, 0.000000000000
668, 0.099690440000, 0.036563840000, 0.000000000000
669, 0.093330610000, 0.034200480000, 0.000000000000
670, 0.087400000000, 0.032000000000, 0.000000000000
671, 0.081900960000, 0.029962610000, 0.000000000000
672, 0.076804280000, 0.028076640000, 0.000000000000
673, 0.072077120000, 0.026329360000, 0.000000000000
674, 0.067686640000, 0.024708050000, 0.000000000000
675, 0.063600000000, 0.023200000000, 0.000000000000
676, 0.059806850000, 0.021800770000, 0.000000000000
677, 0.056282160000, 0.020501120000, 0.000000000000
678, 0.052971040000, 0.019281080000, 0.000000000000
679, 0.049818610000, 0.018120690000, 0.000000000000
680, 0.046770000000, 0.017000000000, 0.000000000000
681, 0.043784050000, 0.015903790000, 0.000000000000
682, 0.040875360000, 0.014837180000, 0.000000000000
683, 0.038072640000, 0.013810680000, 0.000000000000
684, 0.035404610000, 0.012834780000, 0.000000000000
685, 0.032900000000, 0.011920000000, 0.000000000000
686, 0.030564190000, 0.011068310000, 0.000000000000
687, 0.028380560000, 0.010273390000, 0.000000000000
688, 0.026344840000, 0.009533311000, 0.000000000000
689, 0.024452750000, 0.008846157000, 0.000000000000
690, 0.022700000000, 0.008210000000, 0.000000000000
691, 0.021084290000, 0.007623781000, 0.000000000000
692, 0.019599880000, 0.007085424000, 0.000000000000
693, 0.018237320000, 0.006591476000, 0.000000000000
694, 0.016987170000, 0.006138485000, 0.000000000000
695, 0.015840000000, 0.005723000000, 0.000000000000
696, 0.014790640000, 0.005343059000, 0.000000000000
697, 0.013831320000, 0.004995796000, 0.000000000000
698, 0.012948680000, 0.004676404000, 0.000000000000
699, 0.012129200000, 0.004380075000, 0.000000000000
700, 0.011359160000, 0.004102000000, 0.000000000000
701, 0.010629350000, 0.003838453000, 0.000000000000
702, 0.009938846000, 0.003589099000, 0.000000000000
703, 0.009288422000, 0.003354219000, 0.000000000000
704, 0.008678854000, 0.003134093000, 0.000000000000
705, 0.008110916000, 0.002929000000, 0.000000000000
706, 0.007582388000, 0.002738139000, 0.000000000000
707, 0.007088746000, 0.002559876000, 0.000000000000
708, 0.006627313000, 0.002393244000, 0.000000000000
709, 0.006195408000, 0.002237275000, 0.000000000000
710, 0.005790346000, 0.002091000000, 0.000000000000
711, 0.005409826000, 0.001953587000, 0.000000000000
712, 0.005052583000, 0.001824580000, 0.000000000000
713, 0.004717512000, 0.001703580000, 0.000000000000
714, 0.004403507000, 0.001590187000, 0.000000000000
715, 0.004109457000, 0.001484000000, 0.000000000000
716, 0.003833913000, 0.001384496000, 0.000000000000
717, 0.003575748000, 0.001291268000, 0.000000000000
718, 0.003334342000, 0.001204092000, 0.000000000000
719, 0.003109075000, 0.001122744000, 0.000000000000
720, 0.002899327000, 0.001047000000, 0.000000000000
721, 0.002704348000, 0.000976589600, 0.000000000000
722, 0.002523020000, 0.000911108800, 0.000000000000
723, 0.002354168000, 0.000850133200, 0.000000000000
724, 0.002196616000, 0.000793238400, 0.000000000000
725, 0.002049190000, 0.000740000000, 0.000000000000
726, 0.001910960000, 0.000690082700, 0.000000000000
727, 0.001781438000, 0.000643310000, 0.000000000000
728, 0.001660110000, 0.000599496000, 0.000000000000
729, 0.001546459000, 0.000558454700, 0.000000000000
730, 0.001439971000, 0.000520000000, 0.000000000000
731, 0.001340042000, 0.000483913600, 0.000000000000
732, 0.001246275000, 0.000450052800, 0.000000000000
733, 0.001158471000, 0.000418345200, 0.000000000000
734, 0.001076430000, 0.000388718400, 0.000000000000
735, 0.000999949300, 0.000361100000, 0.000000000000
736, 0.000928735800, 0.000335383500, 0.000000000000
737, 0.000862433200, 0.000311440400, 0.000000000000
738, 0.000800750300, 0.000289165600, 0.000000000000
739, 0.000743396000, 0.000268453900, 0.000000000000
740, 0.000690078600, 0.000249200000, 0.000000000000
741, 0.000640515600, 0.000231301900, 0.000000000000
742, 0.000594502100, 0.000214685600, 0.000000000000
743, 0.000551864600, 0.000199288400, 0.000000000000
744, 0.000512429000, 0.000185047500, 0.000000000000
745, 0.000476021300, 0.000171900000, 0.000000000000
746, 0.000442453600, 0.000159778100, 0.000000000000
747, 0.000411511700, 0.000148604400, 0.000000000000
748, 0.000382981400, 0.000138301600, 0.000000000000
749, 0.000356649100, 0.000128792500, 0.000000000000
750, 0.000332301100, 0.000120000000, 0.000000000000
751, 0.000309758600, 0.000111859500, 0.000000000000
752, 0.000288887100, 0.000104322400, 0.000000000000
753, 0.000269539400, 0.000097335600, 0.000000000000
754, 0.000251568200, 0.000090845870, 0.000000000000
755, 0.000234826100, 0.000084800000, 0.000000000000
756, 0.000219171000, 0.000079146670, 0.000000000000
757, 0.000204525800, 0.000073858000, 0.000000000000
758, 0.000190840500, 0.000068916000, 0.000000000000
759, 0.000178065400, 0.000064302670, 0.000000000000
760, 0.000166150500, 0.000060000000, 0.000000000000
761, 0.000155023600, 0.000055981870, 0.000000000000
762, 0.000144621900, 0.000052225600, 0.000000000000
763, 0.000134909800, 0.000048718400, 0.000000000000
764, 0.000125852000, 0.000045447470, 0.000000000000
765, 0.000117413000, 0.000042400000, 0.000000000000
766, 0.000109551500, 0.000039561040, 0.000000000000
767, 0.000102224500, 0.000036915120, 0.000000000000
768, 0.000095394450, 0.000034448680, 0.000000000000
769, 0.000089023900, 0.000032148160, 0.000000000000
770, 0.000083075270, 0.000030000000, 0.000000000000
771, 0.000077512690, 0.000027991250, 0.000000000000
772, 0.000072313040, 0.000026113560, 0.000000000000
773, 0.000067457780, 0.000024360240, 0.000000000000
774, 0.000062928440, 0.000022724610, 0.000000000000
775, 0.000058706520, 0.000021200000, 0.000000000000
776, 0.000054770280, 0.000019778550, 0.000000000000
777, 0.000051099180, 0.000018452850, 0.000000000000
778, 0.000047676540, 0.000017216870, 0.000000000000
779, 0.000044485670, 0.000016064590, 0.000000000000
780, 0.000041509940, 0.000014990000, 0.000000000000
781, 0.000038733240, 0.000013987280, 0.000000000000
782, 0.000036142030, 0.000013051550, 0.000000000000
783, 0.000033723520, 0.000012178180, 0.000000000000
784, 0.000031464870, 0.000011362540, 0.000000000000
785, 0.000029353260, 0.000010600000, 0.000000000000
786, 0.000027375730, 0.000009885877, 0.000000000000
787, 0.000025524330, 0.000009217304, 0.000000000000
788, 0.000023793760, 0.000008592362, 0.000000000000
789, 0.000022178700, 0.000008009133, 0.000000000000
790, 0.000020673830, 0.000007465700, 0.000000000000
791, 0.000019272260, 0.000006959567, 0.000000000000
792, 0.000017966400, 0.000006487995, 0.000000000000
793, 0.000016749910, 0.000006048699, 0.000000000000
794, 0.000015616480, 0.000005639396, 0.000000000000
795, 0.000014559770, 0.000005257800, 0.000000000000
796, 0.000013573870, 0.000004901771, 0.000000000000
797, 0.000012654360, 0.000004569720, 0.000000000000
798, 0.000011797230, 0.000004260194, 0.000000000000
799, 0.000010998440, 0.000003971739, 0.000000000000
800, 0.000010253980, 0.000003702900, 0.000000000000
801, 0.000009559646, 0.000003452163, 0.000000000000
802, 0.000008912044, 0.000003218302, 0.000000000000
803, 0.000008308358, 0.000003000300, 0.000000000000
804, 0.000007745769, 0.000002797139, 0.000000000000
805, 0.000007221456, 0.000002607800, 0.000000000000
806, 0.000006732475, 0.000002431220, 0.000000000000
807, 0.000006276423, 0.000002266531, 0.000000000000
808, 0.000005851304, 0.000002113013, 0.000000000000
809, 0.000005455118, 0.000001969943, 0.000000000000
810, 0.000005085868, 0.000001836600, 0.000000000000
811, 0.000004741466, 0.000001712230, 0.000000000000
812, 0.000004420236, 0.000001596228, 0.000000000000
813, 0.000004120783, 0.000001488090, 0.000000000000
814, 0.000003841716, 0.000001387314, 0.000000000000
815, 0.000003581652, 0.000001293400, 0.000000000000
816, 0.000003339127, 0.000001205820, 0.000000000000
817, 0.000003112949, 0.000001124143, 0.000000000000
818, 0.000002902121, 0.000001048009, 0.000000000000
819, 0.000002705645, 0.000000977058, 0.000000000000
820, 0.000002522525, 0.000000910930, 0.000000000000
821, 0.000002351726, 0.000000849251, 0.000000000000
822, 0.000002192415, 0.000000791721, 0.000000000000
823, 0.000002043902, 0.000000738090, 0.000000000000
824, 0.000001905497, 0.000000688110, 0.000000000000
825, 0.000001776509, 0.000000641530, 0.000000000000
826, 0.000001656215, 0.000000598090, 0.000000000000
827, 0.000001544022, 0.000000557575, 0.000000000000
828, 0.000001439440, 0.000000519808, 0.000000000000
829, 0.000001341977, 0.000000484612, 0.000000000000
830, 0.000001251141, 0.000000451810, 0.000000000000
Modifié en dernier par Emmanuel Piat le 10 févr. 2026, 15:56, modifié 2 fois.
-
Emmanuel Piat
- 34 dB
- Messages : 72
- Enregistré le : 11 janv. 2026, 11:26
Re: Les sondes de calibration
Voici le script Scilab "Lamp2.sce" à mettre dans le même dossier que les 2 fichiers précédents.
Vous devez remplacer le chemin de la 1ère ligne du script par celui qui correspond à ce dossier :
cd('G:/Privé/Etalonnage vidéoprojecteur/');
Attention, il faut utiliser des "/" comme sous Linux.
Dans l'IDE de Scilab, Sélectionnez "Applications" dans la barre de menu, puis "SciNotes". Dans SciNotes, ouvrez le fichier "Lamp2.sce" puis cliquez sur l'icône Exécuter (petit triangle orienté vers la droite). Les figures apparaîtront et des messages s'écriront dans la console de Scilab.
Le code est composé au début d'un tas de fonctions utiles pour le script. L'IA m'a aidé à en écrire certaines.
Après la def. des fonctions il y a le script qui est long mais basique : c'est des calculs élémentaires de spectres ou d'erreurs relative et plein de plots pour les figures.
Scilab est un super outil gratuit de calcul numérique avec plein de toolboxes associées. Ca se programme sans douleur et c'est parfait pour faire du prototypage rapide de traitements numériques. Si vous avez des besoins en calculs, le mieux pour le prendre en main est de récupérer un tuto pdf. Il y en a plein internet à destination des étudiants. Tous ces tutos sont très bien écrits.
Vous devez remplacer le chemin de la 1ère ligne du script par celui qui correspond à ce dossier :
cd('G:/Privé/Etalonnage vidéoprojecteur/');
Attention, il faut utiliser des "/" comme sous Linux.
Dans l'IDE de Scilab, Sélectionnez "Applications" dans la barre de menu, puis "SciNotes". Dans SciNotes, ouvrez le fichier "Lamp2.sce" puis cliquez sur l'icône Exécuter (petit triangle orienté vers la droite). Les figures apparaîtront et des messages s'écriront dans la console de Scilab.
Le code est composé au début d'un tas de fonctions utiles pour le script. L'IA m'a aidé à en écrire certaines.
Après la def. des fonctions il y a le script qui est long mais basique : c'est des calculs élémentaires de spectres ou d'erreurs relative et plein de plots pour les figures.
Scilab est un super outil gratuit de calcul numérique avec plein de toolboxes associées. Ca se programme sans douleur et c'est parfait pour faire du prototypage rapide de traitements numériques. Si vous avez des besoins en calculs, le mieux pour le prendre en main est de récupérer un tuto pdf. Il y en a plein internet à destination des étudiants. Tous ces tutos sont très bien écrits.
Code : Tout sélectionner
// ###########################################
// ## Script: Modélisation lampe halogène 2 ##
// ###########################################
cd('G:/Privé/Etalonnage vidéoprojecteur/');
// Nettoyage console et variables Scilab
clc; clear;
////////////////////////////////////////
// Définition des fonctions utilisées //
////////////////////////////////////////
// --- Filtre de Savitzky-Golay vectorisé ---
// ------------------------------------------
// Ce filtre lisse un signal en ajustant un polynôme par moindres carrés sur une fenêtre glissante
function y_filtered = savitzky_golay(y, span, degree, order)
// y : vecteur du signal (ligne ou colonne)
// span : taille de la fenêtre (doit être un entier impair)
// degree : ordre du polynôme d'ajustement
// order : (optionnel) ordre de la dérivée (0 = lissage, 1 = dérivée première, etc.)
// Défaut = 0.
[lhs, rhs] = argn(0);
if rhs < 4 then order = 0; end // Par défaut, lissage simple
// 1. Vérifications de base
if modulo(span, 2) == 0 then
error("La taille de la fenêtre (span) doit être impaire.");
end
if degree >= span then
error("Le degré du polynôme doit être strictement inférieur à la fenêtre (span).");
end
// Forcer y en vecteur colonne pour les calculs
y_is_row = (size(y, 1) == 1);
if y_is_row then y = y'; end
n = length(y);
half_win = (span - 1) / 2;
// 2. Calcul des coefficients (Matrice de Vandermonde)
// On centre la fenêtre sur 0 : x = [-half_win, ..., 0, ..., half_win]
x = (-half_win:half_win)';
// Construction de la matrice Design A (Vandermonde)
// A_ij = x_i^j
A = ones(span, degree + 1);
for k = 1:degree
A(:, k+1) = x .^ k;
end
// Calcul de la pseudo-inverse : C = (A' * A)^-1 * A'
// C contient les coefficients pour estimer c0, c1, ... cn
// C = inv(A' * A) * A';
C = pinv(A); // calcul optimisé si A' * A est mal conditionnée
// Les coefficients du filtre correspondent à la ligne relative à l'ordre demandé
// Pour le lissage (ordre 0), c'est la 1ère ligne.
// Pour la dérivée 1ère, c'est la 2ème ligne, mais il faut multiplier par factorielle !
coeffs = C(order + 1, :) * factorial(order);
// 3. Gestion des bords (Padding par réflexion)
// Pour éviter les effets de bord, on "reflète" le signal aux extrémités
pad_start = y(half_win+1:-1:2); // Reflet du début
pad_end = y($-1:-1:$-half_win); // Reflet de la fin
y_padded = [pad_start; y; pad_end];
// 4. Convolution vectorisée
// On applique les coefficients calculés sur tout le signal d'un coup par convolution
// Note: convol inverse le deuxième argument, mais SG est symétrique pour le lissage,
// donc il faut inverser 'coeffs'.
y_conv = convol(y_padded, coeffs($:-1:1)); // format colonne
// 5. Extraction de la partie utile (suppression du padding)
// La convolution ajoute (span-1) points. On doit couper au bon endroit.
start_idx = 2 * half_win + 1;
end_idx = start_idx + n - 1;
y_filtered = y_conv(start_idx:end_idx); // format colonne
// Restitution de l'orientation originale (ligne ou colonne)
if ~y_is_row then y_filtered = y_filtered'; end
endfunction
// --- Loi de Planck ---
// ---------------------
function L = planck_law(lambda, T)
// T : température en Kelvin
// lambda : longueur d'onde en nm
// L : luminance énergétique spectrale par unité de fréquence en $W m^{-2} sr^{-1} Hz^{-1}$
h = 6.626e-34; // Constante de Planck (J s)
c = 2.998e8; // Vitesse de la lumière (m/s)
k = 1.381e-23; // Constante de Boltzmann (J/K))
lambda_m = lambda * 1e-9;
L = (2*h*c^2) ./ (lambda_m.^5 .* (exp((h*c)./(lambda_m*k*T)) - 1));
endfunction
// --- Loi de Planck normalisée entre 0 et 1 ---
// ---------------------------------------------
function Lnorm = planck_law_norm(lambda, T)
// T température en Kelvin
// lambda : longueur d'onde en nm
// Lnorm : entre 0 et 1 sans unité
L = planck_law(lambda,T);
Lnorm = L ./ max(L);
endfunction
// --- Calcul chromaticité (x,y) dans l'espace CIE 1931 ---
// --------------------------------------------------------
function [x,y] = calc_chromaticite(spectre, cmf)
// spectre : vecteur colonne contenant les valeurs du spectre
// cmf : color matching functions CIE 1931
// cmf(:,1) : longueurs d'onde en nm qui doivent être les mêmes que pour spectre (attention)
// cmf(:,2) : $\overline{x}$
// cmf(:,3) : $\overline{y}$
// cmf(:,4) : $\overline{z}$
// Pas d'interpolation du spectre de la lampe car pas de 1nm comme pour la CIE
// l_cie = CMF(:,1);
// S_interp = interp1(lambda, spectrum, l_cie, 'spline');
// Calcul des composantes tristimulus (Intégration numérique)
X = sum(spectre .* cmf(:,2));
Y = sum(spectre .* cmf(:,3));
Z = sum(spectre .* cmf(:,4));
// Coordonnées chromatiques x, y
x = X / (X + Y + Z);
y = Y / (X + Y + Z);
endfunction
// --- Calcul de la CCT en utilisant la méthode du NIST avec recherche rapide (Golden Section Search) ---
// En métrologie, on considère qu'à 10000 K, une incertitude de ±10 K est le "Gold Standard".
// Valeurs tests possibles :
// x = 0.5857 y = 0.3931 CCT: 1500 K Duv:0
// Illuminant A x = 0.44757 y = 0.40745 CCT: 2856 K Duv:0
// x = 0.5267 y = 0.4133 CCT: 2000 K Duv:0
// x = 0.4500 y = 0.4200 CCT: 2830 K Duv~0.005
// Illuminant D50 x = 0.3457 y = 0.3585 CCT: 5003 K
// Illuminant D65 x = 0.3127 y = 0.3290 CCT: 6504 K Duv:0.003
// x = 0.2850 y = 0.2750 CCT: 10000 K Duv < 0
// x = 0.28059 y = 0.2885 CCT: 10000 K Duv:0
// x = 0.1800 y = 0.2635 CCT:~100000 K
// --------------------------------------------------------------
function [cct, duv]=calcul_CCT_Optimise(x, y, cmf)
// x : coordonnée chromatique x dans l'espace CIE 1931
// y : coordonnée chromatique y dans l'espace CIE 1931
// cmf : color matching functions CIE 1931
// cmf(:,1) : longueurs d'onde en nm
// cmf(:,2) : $\overline{x}$
// cmf(:,3) : $\overline{y}$
// cmf(:,4) : $\overline{z}$
// 1. Initialisation
// Constante de radiation (échelle CIE ITS-90)
c2 = 1.4388e-2; // Prendre 1.4380e-2 si ancien standard
// Conversion (x,y) de la source -> CIE 1960 (u,v)
denom = -2*x + 12*y + 3;
us = 4*x / denom;
vs = 6*y / denom;
// Structure cmf : Col 1=lambda, Col 2=x_bar, Col 3=y_bar, Col 4=z_bar
wl = cmf(:,1); // longueurs d'onde en nm
L_m = wl * 1e-9; // longueurs d'onde en m
// 2. Fonction de distance locale
function d2=f_dist(T)
spectre = (L_m .^ -5) ./ (exp(c2 ./ (L_m * T)) - 1);
// Utilisation correcte des colonnes 2, 3, 4
X = sum(spectre .* cmf(:,2));
Y = sum(spectre .* cmf(:,3));
Z = sum(spectre .* cmf(:,4));
dp = X + 15*Y + 3*Z;
up = 4*X / dp;
vp = 6*Y / dp;
d2 = (us - up)^2 + (vs - vp)^2;
endfunction
// 3. Recherche par Section Dorée
a = 1000;
b = 25000;
tau = (sqrt(5) - 1) / 2;
eps = 0.01;
x1 = a + (1 - tau) * (b - a);
x2 = a + tau * (b - a);
f1 = f_dist(x1);
f2 = f_dist(x2);
while (b - a) > eps
if f1 < f2 then
b = x2; x2 = x1; f2 = f1;
x1 = a + (1 - tau) * (b - a);
f1 = f_dist(x1);
else
a = x1; x1 = x2; f1 = f2;
x2 = a + tau * (b - a);
f2 = f_dist(x2);
end
end
cct = (a + b) / 2;
// 4. Calcul final de Duv (signé)
spectre_f = (L_m .^ -5) ./ (exp(c2 ./ (L_m * cct)) - 1);
Xf = sum(spectre_f .* cmf(:,2));
Yf = sum(spectre_f .* cmf(:,3));
Zf = sum(spectre_f .* cmf(:,4));
df = Xf + 15*Yf + 3*Zf;
uf = 4*Xf / df;
vf = 6*Yf / df;
duv_abs = sqrt((us - uf)^2 + (vs - vf)^2);
// Calcul de la tangente à la courbe au point CCT
// On prend un point à CCT + 1K pour avoir la direction locale
T_eps = cct + 1.0;
spectre_t = (L_m .^ -5) ./ (exp(c2 ./ (L_m * T_eps)) - 1);
Xt = sum(spectre_t .* cmf(:,2)); Yt = sum(spectre_t .* cmf(:,3)); Zt = sum(spectre_t .* cmf(:,4));
dt = Xt + 15*Yt + 3*Zt; ut = 4*Xt / dt; vt = 6*Yt / dt;
// Vecteur tangent (T) : va du point CCT vers CCT+1K
du_t = ut - uf;
dv_t = vt - vf;
// Vecteur source (S) : va du point Planck vers la source mesurée
du_s = us - uf;
dv_s = vs - vf;
// PRODUIT VECTORIEL 2D : det([T, S])
// La convention standard dans l'espace (u,v) de la CIE 1960 donne Duv > 0 (Vert)
// quand le point est à "gauche" de la courbe en progressant vers les hautes températures.
cp = du_t * dv_s - dv_t * du_s;
if cp < 0 then
duv = duv_abs; // Vert
else
duv = -duv_abs; // Magenta
end
// 5. AFFICHAGE
printf("\n--- RESULTAT OHNO (NIST) ---\n");
printf("Coordonnées Source : u=%.4f, v=%.4f\n", us, vs);
printf("Point Planck le plus proche (%.1f K) : u=%.4f, v=%.4f\n", cct, uf, vf);
printf(">> CCT : %.1f K\n", cct);
printf(">> Duv : %.5f\n", duv);
if abs(duv) < 0.0054 then
printf("Fiabilité : EXCELLENTE (Proche du corps noir).\n");
elseif abs(duv) <= 0.05 then
printf("Fiabilité : ACCEPTABLE (Usage indicatif uniquement).\n");
else
printf("ATTENTION : Invalide (Duv > 0.05). La source est trop colorée.\n");
end
endfunction
// --- Tracé du lieu Planckien et du positionement de la source dans l'espace CIE 1960 uv ---
// ------------------------------------------------------------------------------------------
function tracer_Planck_uv(x_source, y_source, cmf)
// x_source : coordonnée chromatique x dans l'espace CIE 1931
// y_source : coordonnée chromatique y dans l'espace CIE 1931
// cmf : color matching functions CIE 1931
// cmf(:,1) : longueurs d'onde en nm
// cmf(:,2) : $\overline{x}$
// cmf(:,3) : $\overline{y}$
// cmf(:,4) : $\overline{z}$
// 1. Paramètres
c2 = 1.4388e-2;
wl = cmf(:,1);
L_m = wl * 1e-9;
// 2. Génération de la courbe de Planck (de 1000K à 25000K)
temps = [1000:100:2000, 2500:500:10000, 12000:2000:25000];
u_p = []; v_p = [];
for T = temps
spectre = (L_m .^ -5) ./ (exp(c2 ./ (L_m * T)) - 1);
X = sum(spectre .* cmf(:,2));
Y = sum(spectre .* cmf(:,3));
Z = sum(spectre .* cmf(:,4));
denom = X + 15*Y + 3*Z;
u_p = [u_p, 4*X / denom];
v_p = [v_p, 6*Y / denom];
end
// 3. Conversion du source (x,y) vers (u,v)
d_s = -2*x_source + 12*y_source + 3;
us = 4*x_source / d_s;
vs = 6*y_source / d_s;
// 4. Création de la figure dans la fenêtre 0
scf(0); clf();
plot(u_p, v_p, 'b-o', 'LineWidth', 1); // Courbe de Planck en bleu
plot(us, vs, 'r+', 'MarkerSize', 10, 'LineWidth', 2); // Votre source en rouge
xtitle("Lieu Planckien - Espace CIE 1960 (u, v)", "u", "v");
legend(["Lieu Planckien (1000K-25000K)", "Chromaticité source mesurée"], 4);
xgrid(color("grey"));
// 5. Annotation des températures clés
xstring(u_p(5)+0.003, v_p(5), string(temps(5))+"K");
for i = 10:size(temps, 2)
if modulo(temps(i), 1000) == 0 then
xstring(u_p(i)+0.003, v_p(i), string(temps(i))+"K");
end
end
endfunction
// --- Lecture de la table des color matching functions à partir des données
// officiellez CIE 1931 pour lambda entre 360 à 830 nm par pas de 1 nm ---
// Table d'origine : https://www.cie.co.at/data-tables
// -----------------------------------------------------------------------
function cie_cmf = read_CMF_1931()
cmf_file = "ciexyz31.txt";
if isfile(cmf_file) then
// Lecture du fichier CIE qui a des virgules comme séparateur
// Colonne 1: lambda,
// Colonne 2: $\overline{x}$,
// Colonne 3: $\overline{y}$,
// Colonne 4: $\overline{z}$
cie_cmf = csvRead(cmf_file, ",", ".", "double");
else
disp("Erreur : Fichier ciexyz31.txt introuvable dans " + pwd());
end
endfunction
/////////////////
//Début script //
/////////////////
// Lecture fichier de la lampe 2 dans le domaine VIS (spectre normalisé - 360 à 830 nm - pas de 1 nm)
nom_fichier = "SLS201_Spectrum_Model2_VIS.txt";
fd = mopen(nom_fichier, "r");
if fd == -1 then
disp("ERREUR : Le fichier " + nom_fichier + " est introuvable dans " + pwd());
// lambdas = []; intensite = [];
abort;
end
// Lecture par paires de nombres (ignore les espaces/tabs)
data = mfscanf(-1, fd, "%f %f");
mclose(fd);
lambdas = data(:,1);
intensite = data(:,2);
disp("Fichier spectre lampe lu avec succès : " + string(size(lambdas, 1)) + " points.");
// Normalisation du spectre
intensite = intensite / max(intensite);
// Calcul (x,y) et CCT du spectre non corrigé
CMF = read_CMF_1931();
[x,y] = calc_chromaticite(intensite,CMF);
printf("Chromaticité spectre non corrigé : x = %.5f | y = %.5f\n", x, y);
[CCT, duv] = calcul_CCT_Optimise(x,y,CMF);
// On trace le lieu Planckien et la chromaticité du spectre non corrigé dans l'espace CIE 1960 uv
tracer_Planck_uv(x, y, CMF);
// Loi de Planck normalisée pour T = CCT
BB_CCT = planck_law_norm(lambdas, CCT);
S = "Corps Noir (" + string(CCT) + " K)"; // Pour la légende
// Affichage des spectres pour comparaison (domaine VIS)
// Echelle linéaire
scf(1); clf();
plot(lambdas, BB_CCT, 'r-', 'LineWidth', 1); // Spectre corps noir avec T = CCT
plot(lambdas, intensite, 'b-', 'LineWidth', 1); // Spectre lampe non corrigé
xtitle("Domaine Visible (360-830 nm)", "Longueur d''onde (nm)", "Intensité Normalisée");
xgrid(color("grey"));
legend([S; "Lampe QTH"],4);
// Echelle log10
scf(2); clf();
plot("nl",lambdas, BB_CCT, 'r-', 'LineWidth', 1); // Spectre corps noir avec T = CCT
plot("nl",lambdas, intensite, 'b-', 'LineWidth', 1); // Spectre lampe non corrigé
xtitle("Domaine Visible (360-830 nm)", "Longueur d''onde (nm)", "Intensité Normalisée");
xgrid(color("grey"));
legend([S; "Lampe QTH"],4);
// Calcul de l'écart relatif : (Lampe - CorpsNoir) / CorpsNoir
E_relatif = intensite ./ BB_CCT - 1;
// Affichage des résultats ds la console
printf("\nAnalyse du modèle :\n");
printf("Ecart moyen : %.2f%%\n", mean(E_relatif*100));
printf("Ecart max : %.2f%% à %d nm\n", max(abs(E_relatif*100)), lambdas(find(abs(E_relatif)==max(abs(E_relatif)))));
// Nettoyage du bruit présent sur l'écart relatif
window_size = 41; // Taille de la fenêtre (doit être impaire)
poly_order = 4; // Ordre du polynôme de lissage
E_relatif_nettoye = savitzky_golay(E_relatif, window_size, poly_order);
// Affichage de l'écart relatif en pourcentage
scf(3); clf();
plot(lambdas, E_relatif*100, 'm-', 'LineWidth', 1);
plot(lambdas, E_relatif_nettoye*100, 'k-', 'LineWidth', 1);
xtitle("Surplus d''émission de la lampe par rapport au "+S, "Longueur d''onde (nm)", "Écart relatif (%)");
xgrid();
legend(["Ecart brut"; "Ecart filtré"]);
// Affichage du bruit du spectre
intensite_nettoye = savitzky_golay(intensite, window_size, poly_order);
scf(4); clf();
plot(lambdas, intensite-intensite_nettoye, 'b-', 'LineWidth', 1);
xgrid(color("grey"));
xtitle("Bruit présent sur le spectre de la lampe", "Longueur d''onde (nm)", "Écart relatif (%)")
// Construction de la cible de calibration avec des splines
// 1. Définition des points de contrôle
x_nodes = [360, 380, 400, 424, 457, 495, 580, 636, 830]';
y_nodes = [E_relatif(lambdas==360)-0.2, ..
E_relatif(lambdas==380)+0.01, ..
E_relatif(lambdas==400)+0.033, ..
-0.002, ..
0.014, ..
E_relatif(lambdas==495)+0.0037, ..
E_relatif(lambdas==580)-0.008, ..
E_relatif(lambdas==636)-0.0035, ..
0]'; // On force le 0 à 830nm
// 2. Calcul de la cible
d = splin(x_nodes, y_nodes, "monotone"); // "monotone" évite les oscillations bizarres
E_cible = interp(lambdas, x_nodes, y_nodes, d);
// 3. Affichage de la cible en pourcentage
scf(5); clf();
plot(lambdas, E_relatif*100, 'color', [0.8 0.8 0.8]); // Données réelles (gris)
plot(lambdas, E_relatif_nettoye*100, 'r-', 'LineWidth', 1);
plot(lambdas, E_cible*100, 'b', 'thickness', 1); // Calibration propre (= réponse système)
xgrid(color("grey"));
title("Calibration Instrumentale par Spline - Référence : "+S);
ylabel("Ecart Relatif (%)");
legend(["Ecart Mesuré (Brut)", "Ecart Mesuré (filtré)", "Spline pour calibration"],4);
// 4. Calcul de la correction par rapport au corps noir qui la CCT du spectre mesuré
Correction = (E_cible+1)./(E_relatif+1);
Correction_filtre = (E_cible+1)./(E_relatif_nettoye+1);
scf(6); clf();
plot(lambdas, Correction, 'b', 'thickness', 1);
plot(lambdas, Correction_filtre, 'r', 'thickness', 1);
xgrid(color("grey"));
legend(["Correction brute"; "Correction filtrée"],4);
xtitle("Correction du spectromètre", "Longueur d''onde (nm)", "Écart relatif (%)");
// 5. Calcul du spectre corrigé par rapport au corps noir avec T = 2796 K
BB_2796 = planck_law_norm(lambdas, 2796);
spectre_cor = intensite .* Correction_filtre .* BB_2796 ./ BB_CCT;
[xcor,ycor] = calc_chromaticite(spectre_cor,CMF);
printf("\nRESULTAT DE LA CALIBRATION :\n");
printf("Chromaticité spectre corrigé : x = %.5f | y = %.5f\n", xcor, ycor);
[CCTcor, duv] = calcul_CCT_Optimise(xcor,ycor,CMF);
// 6. Affichage de l'effet de la calibration
Scor = "Spectre corrigé (" + string(CCTcor) + " K)"; // Pour la légende
// Echelle linéaire
scf(7); clf();
plot(lambdas, BB_2796, 'g', 'thickness', 1); // Corps noir 2796 K
plot(lambdas, intensite, 'r', 'thickness', 1); // Le spectre initial
plot(lambdas, spectre_cor, 'b', 'thickness', 1); // La spectre calibré
//gca().data_bounds = [360, 0 ; 830, 1.1];
xgrid(color("grey"));
xtitle("Domaine Visible (360-830 nm)", "Longueur d''onde (nm)", "Intensité Normalisée");
legend(["Corps noir (2796 K)"; "Spectre non corrigé"; Scor],4);
// Echelle log10
scf(8); clf();
plot("nl",lambdas, BB_2796, 'g', 'thickness', 1); // Corps noir 2796 K
plot("nl",lambdas, intensite, 'r', 'thickness', 1); // Le spectre initial
plot("nl",lambdas, spectre_cor, 'b', 'thickness', 1); // La spectre calibré
xgrid(color("grey"));
xtitle("Domaine Visible (360-830 nm)", "Longueur d''onde (nm)", "Intensité Normalisée");
legend(["Corps noir (2796 K)"; "Spectre non corrigé"; Scor],4);
E_relatif_cor = spectre_cor ./ BB_2796 - 1;
scf(9); clf();
plot(lambdas, E_cible*100, 'color', [0.6 0.6 0.6]);
plot(lambdas, E_relatif_cor*100, 'r', 'thickness', 1); // Calibration propre (= réponse système)
xgrid(color("grey"));
xtitle("Surplus d''émission de la lampe par rapport au corps noir (2796 K) selon spectro corrigé", "Longueur d''onde (nm)", "Écart relatif (%)");
legend(["Spline de calibration"; "Ecart au corps noir (2796 K)"],4);
Modifié en dernier par Emmanuel Piat le 10 févr. 2026, 23:44, modifié 6 fois.
-
Emmanuel Piat
- 34 dB
- Messages : 72
- Enregistré le : 11 janv. 2026, 11:26
Re: Les sondes de calibration
Dans le script, j'ai ajouté l'affichage des spectres en échelle log10 sur l'axe des ordonnées. Ca permet de mieux voir ce qu'il se passe pour les petites amplitudes spectrales.
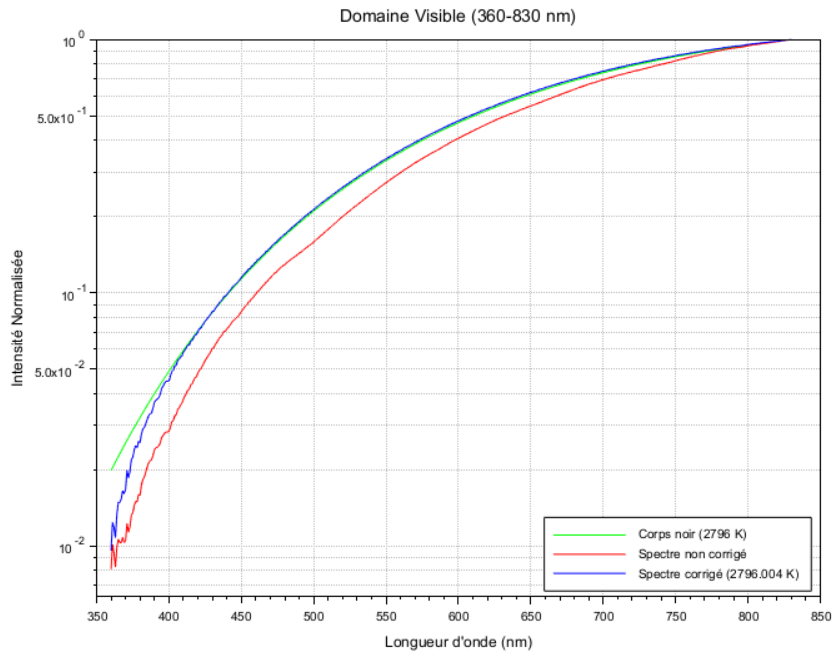

-
Emmanuel Piat
- 34 dB
- Messages : 72
- Enregistré le : 11 janv. 2026, 11:26
Re: Les sondes de calibration
En attendant que j'avance sur le modèle d'une lampe QTH, voici qq considérations pratiques sur la mise en oeuvre de la calib du spectro en intensité relative.
A toute fin utile, je rappelle que je ne suis en rien expert de ces questions. Je suis juste en phase d'acquisition de connaissances, lesquelles resteront forcément très limitées comparé à un expert en radiométrie et en optique. Mon expérience pratique sur ce sujet est également nulle.
Le dispositif de mesure sera constitué de 3 éléments : un spectro, 1 à 2m de fibre optique multimodes et une lentille collimatrice (qui pourrait être un doublet achromatique).
Avec une source fibrée comme la lampe Thorlabs, on peut envisager de compenser seulement les défauts du spectro et de la fibre optique. Comme il y a une optique collimatrice dans la lampe pour concentrer la lumière à l'entrée de la fibre, le flux lumineux émis par l'ampoule sera forcément un peu modifié par ce système optique : le système "lampe" qui émet la lumière n'est pas qu'une simple ampoule QTH : c'est un système plus complexe qui présente forcément des défauts ...
Avec ce type d'approche, on sera en plus obligé de corriger dans un second temps l'influence de la lentille collimatrice du dispositif de mesure ... Pas simple.
Le nouveau modèle de la lampe Thorlabs (vendu depuis 2016) permet de modifier l'optique de sortie pour émettre un flux lumineux vers un dispositif autre qu'une fibre qui pourrait être par exemple le collimateur du futur dispositif de mesure. Dans ce cas, ça permettrait de corriger toute la chaine de mesure en une seule opération. Mais encore une fois, le système "lampe" qui émet la lumière n'est pas qu'une simple ampoule QTH.
Pour info, je possède uniqt l'ancien modèle de cette lampe qui ne peut émettre de la lumière que vers une fibre optique ...
Si on veut que le système "lampe" se ramène uniqt à l'ampoule QTH et son alim, on est obligé d'adopter une autre approche.
Cette autre approche consiste à mettre en oeuvre une ampoule Halogène-Tungstène de la manière la plus stabilisée possible et à éclairer directement le dispositif de mesure avec. Ce faisant, on peut corriger toute la chaine de mesure.
Vous avez une illustration d'une telle mise en oeuvre dans un contexte métrologique (radiométrique) à la page 16 de ce document :
https://www.newport.com/medias/sys_mast ... ources.pdf
Dans les pages suivantes vous trouverez des illustrations de spectres mesurés avec ce principe. La qualité des mesures est impressionnante.
A toute fin utile, je rappelle que je ne suis en rien expert de ces questions. Je suis juste en phase d'acquisition de connaissances, lesquelles resteront forcément très limitées comparé à un expert en radiométrie et en optique. Mon expérience pratique sur ce sujet est également nulle.
Le dispositif de mesure sera constitué de 3 éléments : un spectro, 1 à 2m de fibre optique multimodes et une lentille collimatrice (qui pourrait être un doublet achromatique).
Avec une source fibrée comme la lampe Thorlabs, on peut envisager de compenser seulement les défauts du spectro et de la fibre optique. Comme il y a une optique collimatrice dans la lampe pour concentrer la lumière à l'entrée de la fibre, le flux lumineux émis par l'ampoule sera forcément un peu modifié par ce système optique : le système "lampe" qui émet la lumière n'est pas qu'une simple ampoule QTH : c'est un système plus complexe qui présente forcément des défauts ...
Avec ce type d'approche, on sera en plus obligé de corriger dans un second temps l'influence de la lentille collimatrice du dispositif de mesure ... Pas simple.
Le nouveau modèle de la lampe Thorlabs (vendu depuis 2016) permet de modifier l'optique de sortie pour émettre un flux lumineux vers un dispositif autre qu'une fibre qui pourrait être par exemple le collimateur du futur dispositif de mesure. Dans ce cas, ça permettrait de corriger toute la chaine de mesure en une seule opération. Mais encore une fois, le système "lampe" qui émet la lumière n'est pas qu'une simple ampoule QTH.
Pour info, je possède uniqt l'ancien modèle de cette lampe qui ne peut émettre de la lumière que vers une fibre optique ...
Si on veut que le système "lampe" se ramène uniqt à l'ampoule QTH et son alim, on est obligé d'adopter une autre approche.
Cette autre approche consiste à mettre en oeuvre une ampoule Halogène-Tungstène de la manière la plus stabilisée possible et à éclairer directement le dispositif de mesure avec. Ce faisant, on peut corriger toute la chaine de mesure.
Vous avez une illustration d'une telle mise en oeuvre dans un contexte métrologique (radiométrique) à la page 16 de ce document :
https://www.newport.com/medias/sys_mast ... ources.pdf
Dans les pages suivantes vous trouverez des illustrations de spectres mesurés avec ce principe. La qualité des mesures est impressionnante.

Modifié en dernier par Emmanuel Piat le 10 févr. 2026, 22:31, modifié 3 fois.
-
Emmanuel Piat
- 34 dB
- Messages : 72
- Enregistré le : 11 janv. 2026, 11:26
Re: Les sondes de calibration
La quantité de lumière émise par l'ampoule vers le spectro est "calibrée" par l'ouverture carrée. Elle est collectée par une sphère d'intégration puis transmise au spectro. La lumière qui ne va pas vers le spectro est absorbée par des parois disposées tout autour du banc optique. En condition métrologique, le tout repose sur une table anti-vib (obligatoire lorsqu'on fait des mesures optiques) et la température environnementale est forcément contrôlée.
La sphère d'intégration est située à une distance d = 50 cm de la lampe pour avoir un flux émis par le filament qui soit homogène. L'orientation du filament est importante (voir document). La distance d ne doit pas descendre en dessous de 30 cm d'après le topo explicatif. La sphère d'intégration permet de moyenner la polarisation du flux lumineux de la lampe afin qu'elle affecte le moins possible la réponse du spectro.
Si on remet tout ça dans un contexte de mise en oeuvre "amateur", voici ce qu'on peut recommander :
1. Il faut maniper ds une pièce sans aucune autre source de lumière que l'ampoule (donc pièce entièrement noire si l'ampoule est éteinte)
2. Il faut que l'environnement autour de l'ampoule absorbe le plus possible la lumière dans toutes les directions. S'il le faut, on peut imaginer une boite autour de l'ampoule qui absorbe la lumière au niveau de ses parois internes. Exemple pour s'inspirer :
https://www.newport.com/f/table-top-light-enclosures
3. Il faut que la température de la pièce soit la plus stable possible. Le fait d'utiliser une boite peut améliorer la stabilité thermique autour de l'ampoule. En métrologie, l'approche "poupées russes" est très souvent adoptée pour les dispositifs sensibles aux perturbations thermiques. Il n'est pas rare d'avoir 3 boites imbriquées pour isoler thermiquement un dispositif. C'est très efficace. Ici un équilibre thermique entre la chaleur émise par l'ampoule et ce que le boite dissipe vers l'extérieur doit se faire. Une ventilation naturelle de la boite peut être une solution à envisager.
4. Il faut minimiser les vibrations au niveau de la fibre et du spectro. Deux dalles bétons de terrasse collées avec du silicone et posées sur un bout de vieux matelas (Latex) posé sur le sol aura déjà une efficacité si on pose dessus la boite et le dispositif de mesure. Si vous voulez plus, il suffira de manipuler à 2h du mat. C'est à cette heure-là que l'activité humaine génère le moins de vibration. Le niveau de vibrations sismiques de votre maison sera divisée par un facteur 10 à 100.
5. Il faudra éviter toute présence humaine dans la salle (utilisation de cables USB assez longs pour mettre le PC ds une autre pièce). On trouve facilement des cables USB actifs de 10m ou plus. J'en utilise un ds ma salle HC.
6. Il ne faudra pas marcher pendant les mesures pour ne pas générer de vibrations sismiques solidiennes. Les mesures pourront durer quelques minutes si on moyenne quelques centaines de spectres pour significativement améliorer le rapport S/N du spectro.
7. Il faudra respecter la période de warm-up de l'électronique (alim, spectro, colorimètre) qui peut aller de 45 min à 1h30. La stabilisation thermique de la boite est également importante.
Tout ça peut paraitre exagéré mais ce n'est pas très difficile à respecter et ça permet de minimiser l'influence des facteurs environnementaux qui perturbent la chaine de mesure. En condition de labo, les capteurs que j'utilise sont très sensibles aux perturbations mécaniques (vibrations). La chambre à vide instrumentée qui comporte mes dispositifs de mesure est posée sur cette table anti-vib très performante qui est prévue pour les charges lourdes :
https://www.newport.com/p/M-VIS3036-SG2-325A
Ce genre de table vaut 15 k€. Pour la version active encore plus performante, il faut rajouter 10 k€... Malgré ses performances, le régime sismique résiduel perturbe mes instruments et je suis obligé d'en tenir compte ...
La sphère d'intégration est située à une distance d = 50 cm de la lampe pour avoir un flux émis par le filament qui soit homogène. L'orientation du filament est importante (voir document). La distance d ne doit pas descendre en dessous de 30 cm d'après le topo explicatif. La sphère d'intégration permet de moyenner la polarisation du flux lumineux de la lampe afin qu'elle affecte le moins possible la réponse du spectro.
Si on remet tout ça dans un contexte de mise en oeuvre "amateur", voici ce qu'on peut recommander :
1. Il faut maniper ds une pièce sans aucune autre source de lumière que l'ampoule (donc pièce entièrement noire si l'ampoule est éteinte)
2. Il faut que l'environnement autour de l'ampoule absorbe le plus possible la lumière dans toutes les directions. S'il le faut, on peut imaginer une boite autour de l'ampoule qui absorbe la lumière au niveau de ses parois internes. Exemple pour s'inspirer :
https://www.newport.com/f/table-top-light-enclosures
3. Il faut que la température de la pièce soit la plus stable possible. Le fait d'utiliser une boite peut améliorer la stabilité thermique autour de l'ampoule. En métrologie, l'approche "poupées russes" est très souvent adoptée pour les dispositifs sensibles aux perturbations thermiques. Il n'est pas rare d'avoir 3 boites imbriquées pour isoler thermiquement un dispositif. C'est très efficace. Ici un équilibre thermique entre la chaleur émise par l'ampoule et ce que le boite dissipe vers l'extérieur doit se faire. Une ventilation naturelle de la boite peut être une solution à envisager.
4. Il faut minimiser les vibrations au niveau de la fibre et du spectro. Deux dalles bétons de terrasse collées avec du silicone et posées sur un bout de vieux matelas (Latex) posé sur le sol aura déjà une efficacité si on pose dessus la boite et le dispositif de mesure. Si vous voulez plus, il suffira de manipuler à 2h du mat. C'est à cette heure-là que l'activité humaine génère le moins de vibration. Le niveau de vibrations sismiques de votre maison sera divisée par un facteur 10 à 100.
5. Il faudra éviter toute présence humaine dans la salle (utilisation de cables USB assez longs pour mettre le PC ds une autre pièce). On trouve facilement des cables USB actifs de 10m ou plus. J'en utilise un ds ma salle HC.
6. Il ne faudra pas marcher pendant les mesures pour ne pas générer de vibrations sismiques solidiennes. Les mesures pourront durer quelques minutes si on moyenne quelques centaines de spectres pour significativement améliorer le rapport S/N du spectro.
7. Il faudra respecter la période de warm-up de l'électronique (alim, spectro, colorimètre) qui peut aller de 45 min à 1h30. La stabilisation thermique de la boite est également importante.
Tout ça peut paraitre exagéré mais ce n'est pas très difficile à respecter et ça permet de minimiser l'influence des facteurs environnementaux qui perturbent la chaine de mesure. En condition de labo, les capteurs que j'utilise sont très sensibles aux perturbations mécaniques (vibrations). La chambre à vide instrumentée qui comporte mes dispositifs de mesure est posée sur cette table anti-vib très performante qui est prévue pour les charges lourdes :
https://www.newport.com/p/M-VIS3036-SG2-325A
Ce genre de table vaut 15 k€. Pour la version active encore plus performante, il faut rajouter 10 k€... Malgré ses performances, le régime sismique résiduel perturbe mes instruments et je suis obligé d'en tenir compte ...
Re: Les sondes de calibration
Pour la boîte, il faut prendre garde à la chaleur dégagée par une lampe halogène. Du carton, noir de surcroît, peut facilement prendre feu.
S'il faut renoncer à une boîte, on peut s'inspirer des pare-soleil pour objectifs photo, qui protègent le système de capture de lumière des lumières parasites.
Pour les vibrations, tu parles de capteurs sensibles aux vibrations, mais est-ce le cas de capteurs optiques ? En astrophoto on fait des poses très longues sur des trépieds en plastoc complètement instables, et je n'ai pas entendu dire que le bruit en très faible lumière en était affecté le moins du monde.
En optique on utilise des bancs de mesure stabilisés pour faire de l'interférométrie, où la position du capteur doit être stable à quelques dizaines de nanomètres près.
Quoi qu'il en soit, au besoin, des amateurs ont montré qu'un montage comme tu le proposes, avec des parpaings sur des chambres à air de mobylette, sur le sol d'une cave pour éviter les vibrations d'un plancher, permettaient de réaliser des hologrammes par interférométrie laser aussi bien que sur des bancs d'optique extrêmement chers.
S'il faut renoncer à une boîte, on peut s'inspirer des pare-soleil pour objectifs photo, qui protègent le système de capture de lumière des lumières parasites.
Pour les vibrations, tu parles de capteurs sensibles aux vibrations, mais est-ce le cas de capteurs optiques ? En astrophoto on fait des poses très longues sur des trépieds en plastoc complètement instables, et je n'ai pas entendu dire que le bruit en très faible lumière en était affecté le moins du monde.
En optique on utilise des bancs de mesure stabilisés pour faire de l'interférométrie, où la position du capteur doit être stable à quelques dizaines de nanomètres près.
Quoi qu'il en soit, au besoin, des amateurs ont montré qu'un montage comme tu le proposes, avec des parpaings sur des chambres à air de mobylette, sur le sol d'une cave pour éviter les vibrations d'un plancher, permettaient de réaliser des hologrammes par interférométrie laser aussi bien que sur des bancs d'optique extrêmement chers.
-
Emmanuel Piat
- 34 dB
- Messages : 72
- Enregistré le : 11 janv. 2026, 11:26
Re: Les sondes de calibration
Le problème des vibrations pdt la calib d'un spectro est évoqué ds ce podcast :
https://creators.spotify.com/pod/profil ... on-e1p5dgk
https://creators.spotify.com/pod/profil ... on-e1p5dgk
-
Emmanuel Piat
- 34 dB
- Messages : 72
- Enregistré le : 11 janv. 2026, 11:26
Re: Les sondes de calibration
Tel que je le vois, si on fait une "boite", l'air chaud doit pouvoir s'en échapper vu l'apport calorique de l'ampoule. Plein de designs sont envisageables. L'avantage de la "boite", c'est que la surface à traiter pour absorber la lumière est plus petite que pour une pièce. D'un autre côté, le flux reçu par les parois par unité de surface est supérieur à celui des murs de la pièce. Donc il faut que les parois de la boite absorbent davantage la lumière ... Une structure légère de 1m^3 avec un "toit" surélevé par rapport aux parois latérales et qui déborde un peu sur les bords pourrait convenir. Les bords n'ont pas besoin d'être forcément en dur. Ca pourrait être juste du tissu qui pend comme un rideau et qui est tenu par une structure légère ...
Modifié en dernier par Emmanuel Piat le 11 févr. 2026, 00:03, modifié 1 fois.