Bonjour à tous.
Vous pouvez désormais, si l'envie vous en dit, soutenir SoundPixelLab - Vous retrouverez les informations sur ce lien en dessous
Soutenir SoundPixelLab
Merci à vous !
Vous pouvez désormais, si l'envie vous en dit, soutenir SoundPixelLab - Vous retrouverez les informations sur ce lien en dessous
Soutenir SoundPixelLab
Merci à vous !
Les sondes de calibration
-
Emmanuel Piat
- 28 dB
- Messages : 63
- Enregistré le : 11 janv. 2026, 11:26
Re: Les sondes de calibration
L'analyse du point (2) n'était pas correcte. Je l'ai donc réécrite et j'ai ajouté en bas du post le profil du bruit qui a été calculé ainsi :
- j'ai passé un filtre de Savitzky-Golay sur Smes(lambda) pour obtenir un spectre Smes_filtré(lambda) sans bruit.
- j'ai plotté la différence noise(lambda) = Smes(lambda)-Smes_filtré(lambda) pour chaque lambda.
Le bruit noise(lambda) a une moyenne quasi nulle qui vaut 0.000002.
On voit que le bruit obtenu n'a pas un écart-type constant sur lambda. Le bruit augmente sous 475 nm et il augmente aussi après 500 nm. Donc le gain G(lambda) de la correction appliquée à ce spectro est une fct concave.
- j'ai passé un filtre de Savitzky-Golay sur Smes(lambda) pour obtenir un spectre Smes_filtré(lambda) sans bruit.
- j'ai plotté la différence noise(lambda) = Smes(lambda)-Smes_filtré(lambda) pour chaque lambda.
Le bruit noise(lambda) a une moyenne quasi nulle qui vaut 0.000002.
On voit que le bruit obtenu n'a pas un écart-type constant sur lambda. Le bruit augmente sous 475 nm et il augmente aussi après 500 nm. Donc le gain G(lambda) de la correction appliquée à ce spectro est une fct concave.
-
Emmanuel Piat
- 28 dB
- Messages : 63
- Enregistré le : 11 janv. 2026, 11:26
Re: Les sondes de calibration
Passons aux math...
Rappel des notations :
pour simplifier je note "l" la longueur d'onde lambda.
Smes(l) : le spectre normalisé mesuré qu'il faut corriger
S_cor(l) : le spectre normalisé corrigé qu'on veut calculer (CCT de 2796 K)
BB_2796(l) : le spectre normalisé du corps noir à T = 2796 K
BB_2610(l) : le spectre normalisé du corps noir à T = 2610.8 K
E_2610(l) : l'erreur relative entre Smes(lambda) et BB_2610(lambda)
T(l) : l'erreur relative cible par rapport à BT_2610 (courbe bleue tracé avec des splines)
Contrainte : on veut que T(l) soit également l'erreur relative de S_cor par rapport à BT_2796.
Exprimons E_2610(l), non pas en % mais entre 0 et 1 :
E_2610(l) = (Smes(l) - BB_2610(l)) / BB_2610(l)
E_2610(l) = Smes(l) / BB_2610(l) - 1
=> Smes(l) = (E_2610(l) + 1) x BB_2610(l) (Eq. 1)
Soit S(l) le spectre intermédiaire dont l'erreur relative par rapport à BB_2610 est la cible T :
T(l) = S(l) / BB_2610(l) - 1
=> S(l) = (T(l) + 1) x BB_2610(l) (Eq. 2)
On divise (Eq. 2) par (Eq. 1) :
S(l) / Smes(l) = (T(l) + 1) / (E_2610(l) + 1)
S(l) = Smes(l) x (T(l) + 1) / (E_2610(l) + 1)
On pose Correction(l) = (T(l) + 1) / (E_2610(l) + 1) (Eq. 3)
=> S(l) = Smes(l) x Correction(l) (Eq. 4)
La CCT de S(l) n'est pas 2796 K. Elle est proche de 2610 K (proche va dépendre du choix de T).
On veut que S_cor ait aussi T comme erreur relative par rapport à BB_2796 (c'est la contrainte) :
T(l) = S_cor(l) / BB_2796(l) - 1
=> S_cor(l) = (T(l) + 1) x BB_2796(l) (Eq. 5)
On divise (Eq. 5) par (Eq. 1) :
S_cor(l) / Smes(T) = (T(l) + 1) x BB_2796(l) / ((E_2610(l) + 1) x BB_2610(l))
S_cor(l) = Smes(l) x (T(l) + 1) x BB_2796(l) / ((E_2610(l) + 1) x BB_2610(l))
S_cor(l) = Smes(l) x (T(l) + 1) / (E_2610(l) + 1) x BB_2796(l) / BB_2610(l)
Voici donc la formule de correction de Smes :
=> S_cor(l) = Smes(l) x Correction(l) x BB_2796(l) / BB_2610(l) (Eq. 6)
avec Correction(l) donnée par l'Eq. 3.
La CCT de S_cor(l) est proche de 2796 K (proche va dépendre du choix de T).
Nota : le facteur d'ajustement qui permet de passer de S(l) à S_cor(l) est BB_2796(l) / BB_2610(l) puisqu'on a grâce à l'Eq. 4 :
S_cor(l) = S(l) x BB_2796(l) / BB_2610(l)
Rappel des notations :
pour simplifier je note "l" la longueur d'onde lambda.
Smes(l) : le spectre normalisé mesuré qu'il faut corriger
S_cor(l) : le spectre normalisé corrigé qu'on veut calculer (CCT de 2796 K)
BB_2796(l) : le spectre normalisé du corps noir à T = 2796 K
BB_2610(l) : le spectre normalisé du corps noir à T = 2610.8 K
E_2610(l) : l'erreur relative entre Smes(lambda) et BB_2610(lambda)
T(l) : l'erreur relative cible par rapport à BT_2610 (courbe bleue tracé avec des splines)
Contrainte : on veut que T(l) soit également l'erreur relative de S_cor par rapport à BT_2796.
Exprimons E_2610(l), non pas en % mais entre 0 et 1 :
E_2610(l) = (Smes(l) - BB_2610(l)) / BB_2610(l)
E_2610(l) = Smes(l) / BB_2610(l) - 1
=> Smes(l) = (E_2610(l) + 1) x BB_2610(l) (Eq. 1)
Soit S(l) le spectre intermédiaire dont l'erreur relative par rapport à BB_2610 est la cible T :
T(l) = S(l) / BB_2610(l) - 1
=> S(l) = (T(l) + 1) x BB_2610(l) (Eq. 2)
On divise (Eq. 2) par (Eq. 1) :
S(l) / Smes(l) = (T(l) + 1) / (E_2610(l) + 1)
S(l) = Smes(l) x (T(l) + 1) / (E_2610(l) + 1)
On pose Correction(l) = (T(l) + 1) / (E_2610(l) + 1) (Eq. 3)
=> S(l) = Smes(l) x Correction(l) (Eq. 4)
La CCT de S(l) n'est pas 2796 K. Elle est proche de 2610 K (proche va dépendre du choix de T).
On veut que S_cor ait aussi T comme erreur relative par rapport à BB_2796 (c'est la contrainte) :
T(l) = S_cor(l) / BB_2796(l) - 1
=> S_cor(l) = (T(l) + 1) x BB_2796(l) (Eq. 5)
On divise (Eq. 5) par (Eq. 1) :
S_cor(l) / Smes(T) = (T(l) + 1) x BB_2796(l) / ((E_2610(l) + 1) x BB_2610(l))
S_cor(l) = Smes(l) x (T(l) + 1) x BB_2796(l) / ((E_2610(l) + 1) x BB_2610(l))
S_cor(l) = Smes(l) x (T(l) + 1) / (E_2610(l) + 1) x BB_2796(l) / BB_2610(l)
Voici donc la formule de correction de Smes :
=> S_cor(l) = Smes(l) x Correction(l) x BB_2796(l) / BB_2610(l) (Eq. 6)
avec Correction(l) donnée par l'Eq. 3.
La CCT de S_cor(l) est proche de 2796 K (proche va dépendre du choix de T).
Nota : le facteur d'ajustement qui permet de passer de S(l) à S_cor(l) est BB_2796(l) / BB_2610(l) puisqu'on a grâce à l'Eq. 4 :
S_cor(l) = S(l) x BB_2796(l) / BB_2610(l)
Modifié en dernier par Emmanuel Piat le 09 févr. 2026, 17:08, modifié 2 fois.
-
Emmanuel Piat
- 28 dB
- Messages : 63
- Enregistré le : 11 janv. 2026, 11:26
Re: Les sondes de calibration
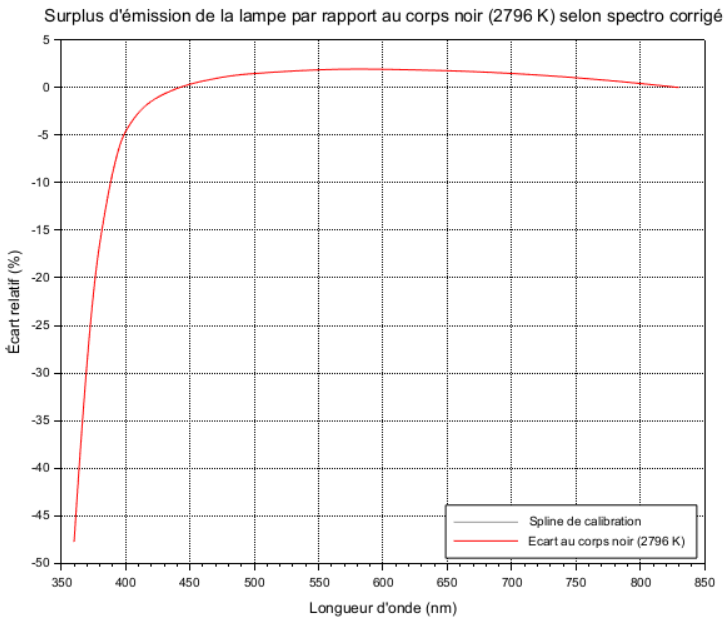
Voici l'écart relatif du spectre corrigé S_cor par rapport à BB_2796. On retrouve bien que c'est la courbe cible tracée avec des splines car les 2 courbes sont superposées.

-
Emmanuel Piat
- 28 dB
- Messages : 63
- Enregistré le : 11 janv. 2026, 11:26
Re: Les sondes de calibration
Tiens il n'y a plus de bruit sur l'erreur relative précédente ! Est-ce normal ?
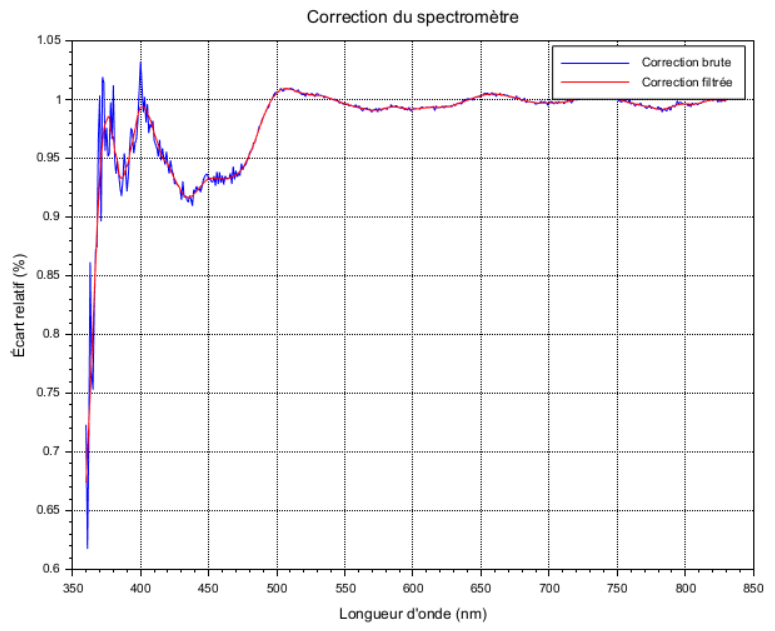
Pour répondre à cette question, voici en bleu la correction totale appliquée à Smes qui est d'après l'Eq. 6 :
Correction(l) x BB_2796(l) / BB_2610(l)
On voit que la courbe bleue est bruitée de manière à compenser très exactement le bruit présent dans Smes. Sauf qu'en pratique le bruit présent dans Smes varie à chaque mesure de nouveau spectre. Donc ce qui a marché une fois ne remarchera pas une 2e fois puisque la correction appliquée est tjrs la même.
En pratique, on évite d'inclure du bruit dans une correction pour ne pas amplifier le bruit déjà présent dans le signal (il peut y avoir des exceptions... Tout dépend du niveau du bruit inclus dans la correction et son impact). Donc ici, on va plutôt utiliser la correction filtrée (en rouge).
Nota : cette correction est un gain G(l). Donc si G(l) = 1 aucune correction n'est appliquée au spectre mesuré Smes(l). On voit ici que la correction varie plus ou moins autour de 1 et elle coupe le signal spectral sous 670 nm.
Pour répondre à cette question, voici en bleu la correction totale appliquée à Smes qui est d'après l'Eq. 6 :
Correction(l) x BB_2796(l) / BB_2610(l)
On voit que la courbe bleue est bruitée de manière à compenser très exactement le bruit présent dans Smes. Sauf qu'en pratique le bruit présent dans Smes varie à chaque mesure de nouveau spectre. Donc ce qui a marché une fois ne remarchera pas une 2e fois puisque la correction appliquée est tjrs la même.
En pratique, on évite d'inclure du bruit dans une correction pour ne pas amplifier le bruit déjà présent dans le signal (il peut y avoir des exceptions... Tout dépend du niveau du bruit inclus dans la correction et son impact). Donc ici, on va plutôt utiliser la correction filtrée (en rouge).
Nota : cette correction est un gain G(l). Donc si G(l) = 1 aucune correction n'est appliquée au spectre mesuré Smes(l). On voit ici que la correction varie plus ou moins autour de 1 et elle coupe le signal spectral sous 670 nm.

Modifié en dernier par Emmanuel Piat le 09 févr. 2026, 17:14, modifié 2 fois.
-
Emmanuel Piat
- 28 dB
- Messages : 63
- Enregistré le : 11 janv. 2026, 11:26
Re: Les sondes de calibration
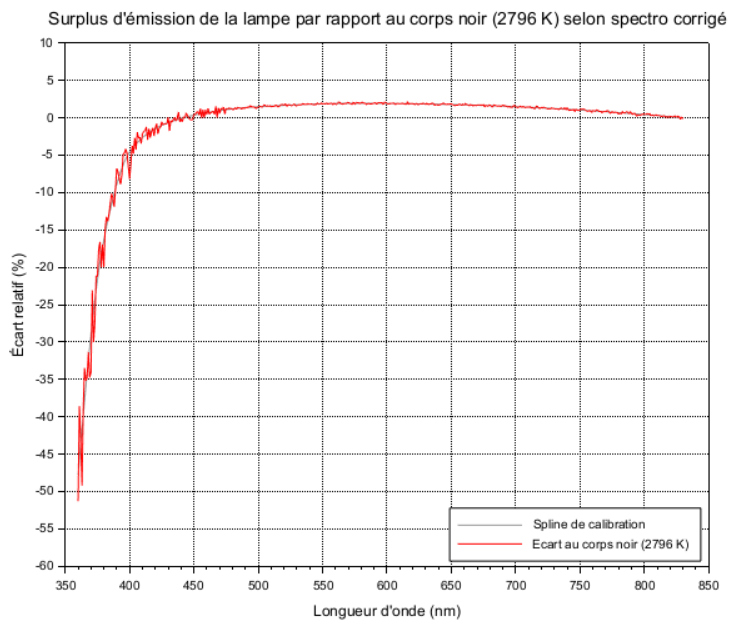
Si on applique la correction filtrée en rouge, on retrouve le bruit sur l'erreur relative et c'est cette situation-là qui est "normale" :

-
Emmanuel Piat
- 28 dB
- Messages : 63
- Enregistré le : 11 janv. 2026, 11:26
Re: Les sondes de calibration
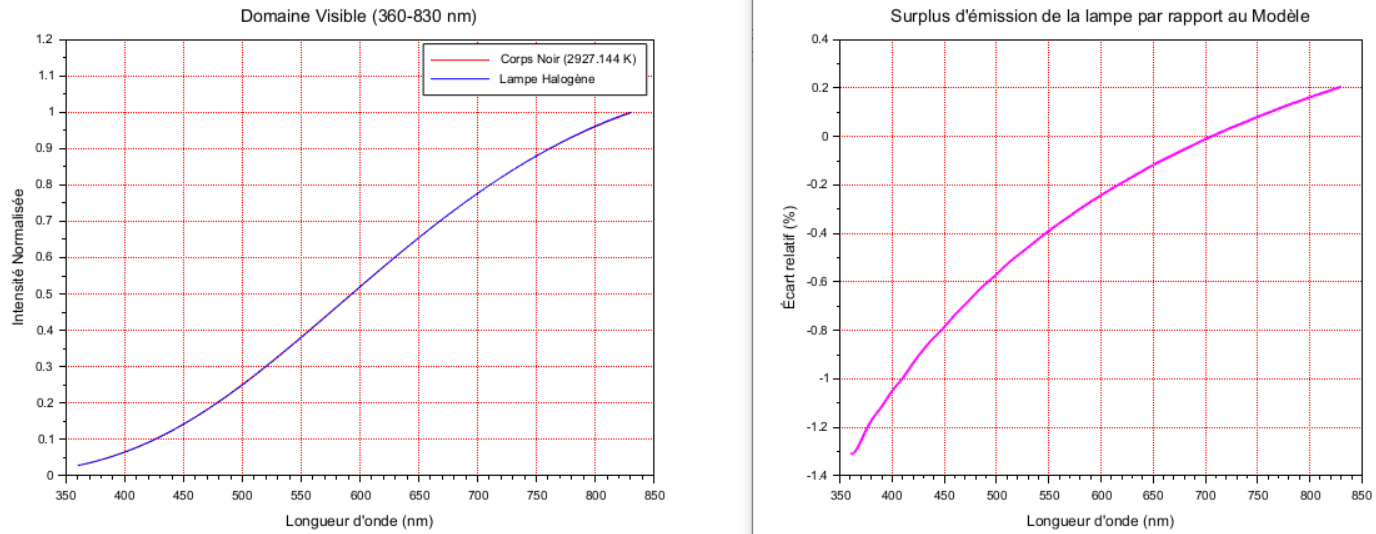
Passons maintenant à la lampe n°1 de Thorlabs. Pour rappel son spectre à une CCT qui vaut 2927.1 K et l'erreur relative entre son spectre et BB_2927 est affichée dans la fig. de droite.

-
Emmanuel Piat
- 28 dB
- Messages : 63
- Enregistré le : 11 janv. 2026, 11:26
Re: Les sondes de calibration
Faut-ll définir une nouvelle cible dans notre contexte de déconvo aveugle ? On ne voit aucun accident sur la forme très régulière de l'erreur relative et cette dernière est faible. Donc, perso, je ne le ferai pas et si la CCT réelle est bien 2796 K (vérifiable avec un colorimètre qui est précis sur les illuminants de type A), je me contenterai juste d'appliquer le facteur d'ajustement des CCT pour déterminer la correction qui sera simplement BB_2796(l) / BB_2927(l).
S_cor(l) = Smes(l) x BB_2796(l) / BB_2927(l)
L'écart relatif du spectre corrigé par rapport cette fois-ci à BB_2796 sera alors tjrs celui de la figure de droite (avec les mêmes valeurs d'erreurs relatives, donc faibles).
Si la CCT réelle de la lampe est xxxx et est différente de 2796, la démarche est strictement la même en remplaçant BB_2796 par BB_xxxx .
S_cor(l) = Smes(l) x BB_2796(l) / BB_2927(l)
L'écart relatif du spectre corrigé par rapport cette fois-ci à BB_2796 sera alors tjrs celui de la figure de droite (avec les mêmes valeurs d'erreurs relatives, donc faibles).
Si la CCT réelle de la lampe est xxxx et est différente de 2796, la démarche est strictement la même en remplaçant BB_2796 par BB_xxxx .
Modifié en dernier par Emmanuel Piat le 09 févr. 2026, 17:04, modifié 3 fois.
-
Emmanuel Piat
- 28 dB
- Messages : 63
- Enregistré le : 11 janv. 2026, 11:26
Re: Les sondes de calibration
Résumé :
dans le contexte de la mesure d'une lampe QTH, le spectre obtenu est sensé être très proche de celui d'un BB si la lampe est correctement mise en oeuvre et peu utilisée. Au fur et à mesure que la lampe vieillit, du tungstène peut se déposer sur les parois de quartz et réduire la transmission dans le bleu.
La différence entre le spectre du BB et le spectre mesuré est induit (i) par l'émissivité du filament de tungstène qui est notamment une fonction de T et de lambda (la géométrie du filament intervient aussi dans la manière dont il rayonne angulairement) et (ii) par tous les défauts de la chaîne acquisition.
Si on veut pouvoir étalonner radiométriquement un spectro en calculant un facteur de correction pour chaque longueur d'onde qui compense les défauts de la chaîne d'acquisition, il faut impérativement disposer d'une lampe étalon dont le spectre est connu et relié au système international d'unités (SI).
Si on peut se contenter d'opérer en relatif (par exemple spectre normalisé à 1 lorsque le projo projette un patch blanc), on peut tenter d'établir une correction en enlevant les défauts présents sur le spectre mesuré. Une première approche très empirique a permis de jeter les bases du calcul de la correction lorsqu'on dispose d'une courbe d'erreur relative E établie grâce à une comparaison avec le spectre normalisé d'un BB à une température T donnée qui est la CCT du spectre non calibré. Lorsque cette courbe d'erreur relative présente des anomalies "criantes", on peut déjà les supprimer.
Pour aller plus loin dans la démarche de la déconvo semi-aveugle, il faut fournir davantage d'information à l'algo de déconvo. Dans ce cas, on n'a pas d'autres choix que de s'appuyer sur un modèle physique de la lampe QTH pour en déduire quel devrait être son spectre relatif et ainsi affiner la courbe cible.
Il faut que je travaille la question et ça va me prendre un peu de temps.
A suivre ...
dans le contexte de la mesure d'une lampe QTH, le spectre obtenu est sensé être très proche de celui d'un BB si la lampe est correctement mise en oeuvre et peu utilisée. Au fur et à mesure que la lampe vieillit, du tungstène peut se déposer sur les parois de quartz et réduire la transmission dans le bleu.
La différence entre le spectre du BB et le spectre mesuré est induit (i) par l'émissivité du filament de tungstène qui est notamment une fonction de T et de lambda (la géométrie du filament intervient aussi dans la manière dont il rayonne angulairement) et (ii) par tous les défauts de la chaîne acquisition.
Si on veut pouvoir étalonner radiométriquement un spectro en calculant un facteur de correction pour chaque longueur d'onde qui compense les défauts de la chaîne d'acquisition, il faut impérativement disposer d'une lampe étalon dont le spectre est connu et relié au système international d'unités (SI).
Si on peut se contenter d'opérer en relatif (par exemple spectre normalisé à 1 lorsque le projo projette un patch blanc), on peut tenter d'établir une correction en enlevant les défauts présents sur le spectre mesuré. Une première approche très empirique a permis de jeter les bases du calcul de la correction lorsqu'on dispose d'une courbe d'erreur relative E établie grâce à une comparaison avec le spectre normalisé d'un BB à une température T donnée qui est la CCT du spectre non calibré. Lorsque cette courbe d'erreur relative présente des anomalies "criantes", on peut déjà les supprimer.
Pour aller plus loin dans la démarche de la déconvo semi-aveugle, il faut fournir davantage d'information à l'algo de déconvo. Dans ce cas, on n'a pas d'autres choix que de s'appuyer sur un modèle physique de la lampe QTH pour en déduire quel devrait être son spectre relatif et ainsi affiner la courbe cible.
Il faut que je travaille la question et ça va me prendre un peu de temps.
A suivre ...
Re: Les sondes de calibration
Petite correction, que me répète THXRD et qui a fini par me rentrer dans le crâne : ma mère ne voit pas l'ultraviolet, mais son opération lui a redonné une vision dans l'extrémité violette du spectre proche de celle d'une personne de 20 ans (source : https://pubmed.ncbi.nlm.nih.gov/8109464/), bien supérieure à la mienne.